#r(theta)=3+8sin theta#
by converting into parametric equations,
#Rightarrow{(x(theta)=r(theta)cos theta=(3+8sin theta)cos theta),(y(theta)=r(theta)sin theta=(3+8sin theta)sin theta):}#
By differentiating with respect to #theta#,
#x'(theta)=8cos theta cdotcos theta+(3+8sin theta)cdot(-sin theta)#
#=8(cos^2theta-sin^2theta)-3sin theta#
#=8cos2theta-3sin theta#
by evaluating at #theta=pi/6#,
#Rightarrow x'(pi/6)=8cos(pi/3)-3sin(pi/6)=4-3/2=5/2#
By differentiating with respect to #theta#,
#y'(theta)=8cos theta cdot sin theta+(3+8sin theta)cdotcos theta#
#=16sin theta cos theta+3cos theta#
#=8sin2theta+3cos theta#
by evaluating at #theta=pi/6#,
#Rightarrow y'(pi/6)=8sin(pi/3)+3cos(pi/6)=4sqrt{3}+{3sqrt{3}}/2={11sqrt{3}}/2#
So, the slope #m# can be found by
#m={dy}/{dx}|_{theta=pi/6}={{dy}/{d theta}|_{theta = pi /6}}/{{dx]/{d theta}|_{theta = pi /6}}={y'(pi/6)}/{x'(pi/6)}={{11sqrt{3}}/{2}}/{{5}/{2}}={11sqrt{3}}/5#
The graph along with its tangent line at #theta=pi/6# looks like:
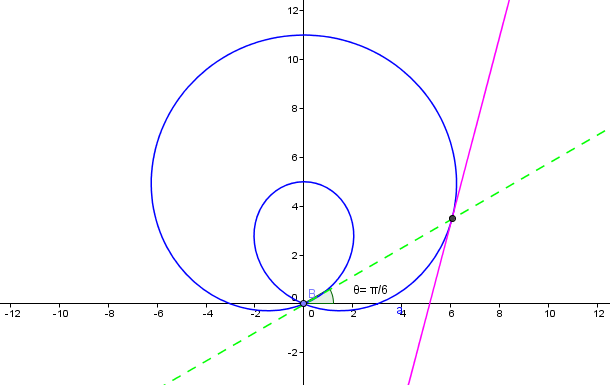
I hope that this was helpful.

