Use implicit differentiation with respect to xx to get: 12x-2y-2x\cdot dy/dx+9y^2\cdot dy/dx=012x−2y−2x⋅dydx+9y2⋅dydx=0 (note that the Chain Rule is used). Now solve for dy/dxdydx to get dy/dx=(2y-12x)/(-2x+9y^2)dydx=2y−12x−2x+9y2. Finally, plug in the point (x,y)=(6,0)(x,y)=(6,0) to get dy/dx|_{(x,y)=(6,0)}=\frac{-72}{-12}=6dydx∣(x,y)=(6,0)=−72−12=6.
By the way, it is worth confirming that (x,y)=(6,0)(x,y)=(6,0) is on the original curve: 6\cdot 6^{2}-2\cdot 6\cdot 0+3\cdot 0^{3}=2166⋅62−2⋅6⋅0+3⋅03=216.
Also, we are assuming yy is a function of xx when we differentiate the original equation. In fact, you may find it more helpful to rewrite the original equation as 6x^2-2xf(x)+3(f(x))^3=2166x2−2xf(x)+3(f(x))3=216 and then, after differentiation, write 12x-2f(x)-2xf'(x)+9(f(x))^2f'(x)=0. Now solve for f'(x) to get f'(x)=(2f(x)-12x)/(-2x+9(f(x))^2) and plug in x=6 and f(6)=0 as above.
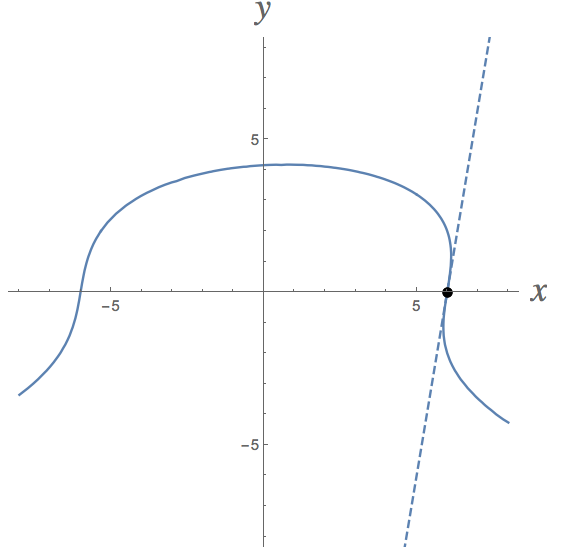
Here's a picture of the situation in this problem. The tangent line at the given point is shown as well (dashed).