Question

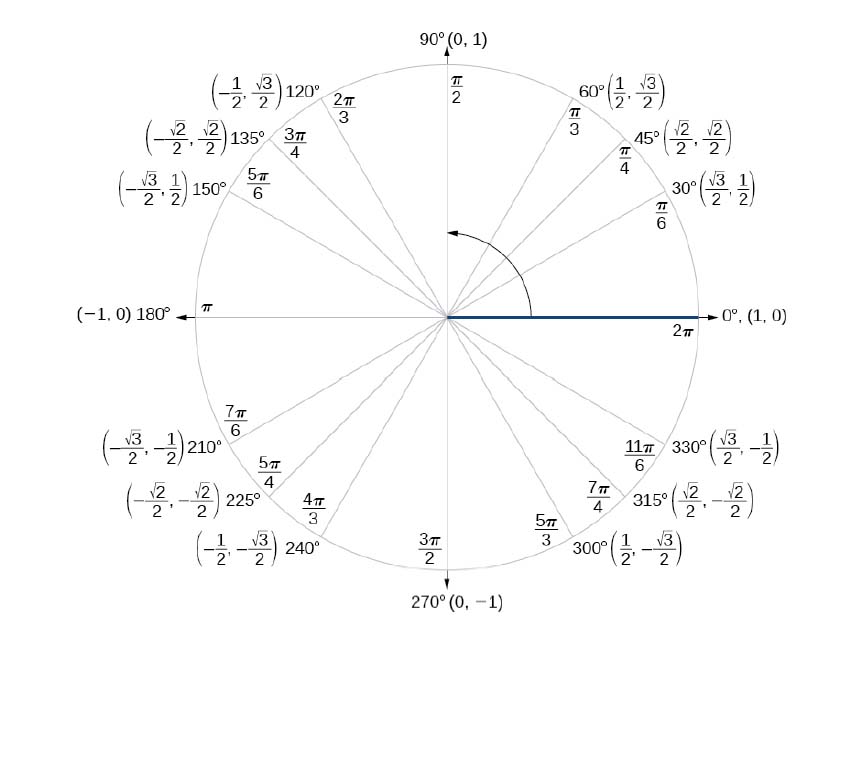
How do you find the solution to `5(costheta+1)=5` if `0<=theta<360`?

Answer 1

`pi/2` and `(3pi)/2`

Explanation:

I assume you know `0<=theta<360` is the same thing as `0<=theta<2pi`

I will solve in Radians which are easier than degrees.

`5(costheta+1)=5` on `0<=theta<2pi`

`5(costheta+1)=5`

divide off the 5:

`costheta+1 = 1`

subtract the 1

`costheta = 0`

now we look at the unit circle:

`costheta=0 " at " pi/2 and (3pi)/2` on the interval `0<=theta<2pi`