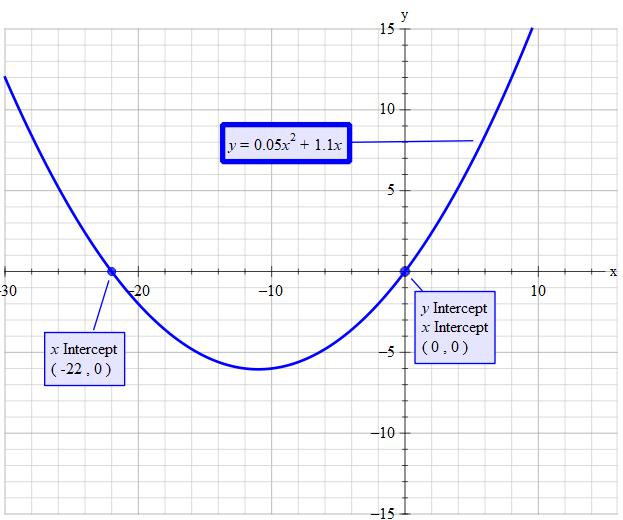
How do you find the solution to the quadratic equation #Y=0.05x^2 + 1.1x#?
1 Answer
Jun 21, 2018
Solving fo
Explanation:
Given:
Set
Factor out
Set
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Using 0 as a place keeper
In this case
Anything times zero is zero so we have:
Thus we have in factored form: