How do you find the standard form of $5 x^{2} + 8 y^{2} + 16 y - 32 = 0$ $5x^2 + 8y^2 + 16y - 32 = 0$ and what kind of a conic is it?

Question

2208 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2016-01-18T20:43:31

First, complete the square ...

$5 x^{2} + 8 y^{2} + 16 y - 32 = 0$ $5x^2 + 8y^2 + 16y - 32 = 0$

$5 x^{2} + 8 (y^{2} + 2 y) = 32$ $5x^2 + 8(y^2 + 2y) = 32$

Now, complete the square ...

$5 x^{2} + 8 (y^{2} + 2 y + 1) = 32 + 8$ $5x^2 + 8(y^2 + 2y+1) = 32+8$

$5 x^{2} + 8 {(y + 1)}^{2} = 40$ $5x^2 + 8(y+1)^2 = 40$

Now, divide both sides by 40 ...

$\frac{x^{2}}{8} + \frac{{(y + 1)}^{2}}{5} = 1$ $x^2/8+(y+1)^2/5=1$

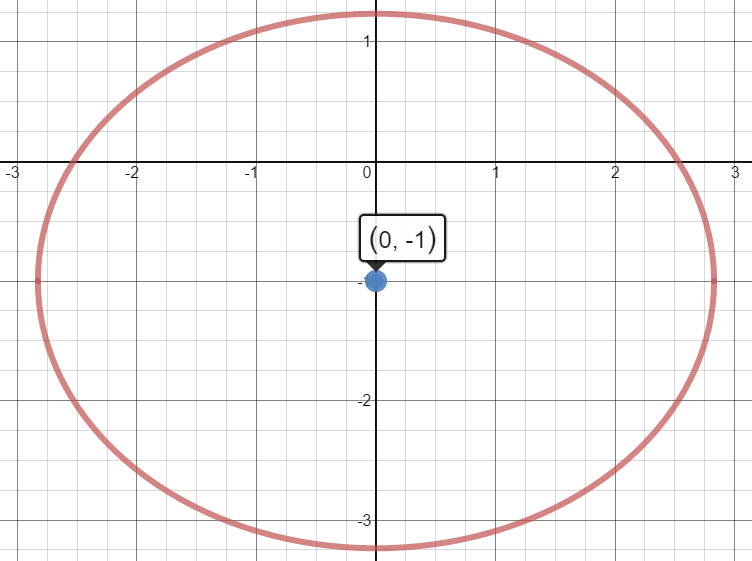
This is an ellipse since the coefficients on x and y are different.

The center $= (0, - 1)$ $=(0,-1)$ .

The major axis is horizontal .

Hope that helped

enter image source here

How do you find the standard form of 5x2+8y2+16y−32=05x^2 + 8y^2 + 16y - 32 = 0 and what kind of a conic is it?