How do you find the tangent lines of parametric curves?
Show that the curve with parametric equations #x=sint# , #y=sin(t+sint)# has two tangent lines at the origin and find their equations. Illustrate by graphing the curve and its tangents.
Show that the curve with parametric equations
1 Answer
Explanation:
First find the derivative:
At the origin we have:
(There are of course more values which may satisfy this but the periodicity of the sine and cosine functions means that the other solutions such as
Checking that these values of
So
For
For
So we have the gradients to our two tangent lines:
We also have a point at which the lines pass through, the origin:
Obviously, for the equation of a straight line
When graphed, they look like this:
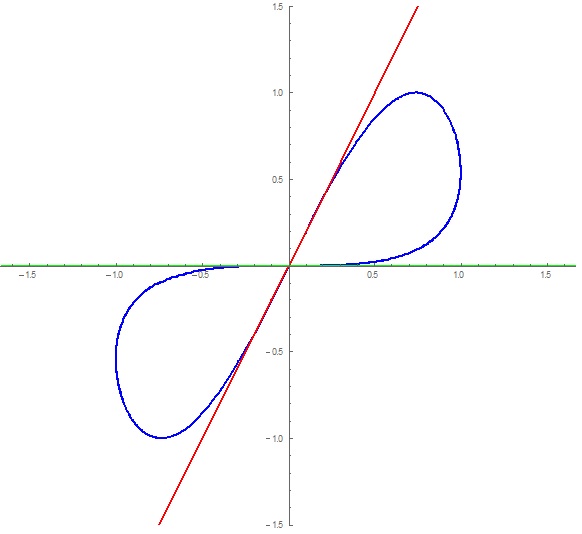
The blue line is the original parametric function and, the red line is

