How do you find the tangent lines to this circle #x^2 + y^2 – 10x + 8y - 8 = 0# passing through the point A (-2,3)?
3 Answers
Here is a graph of the circle and the point:
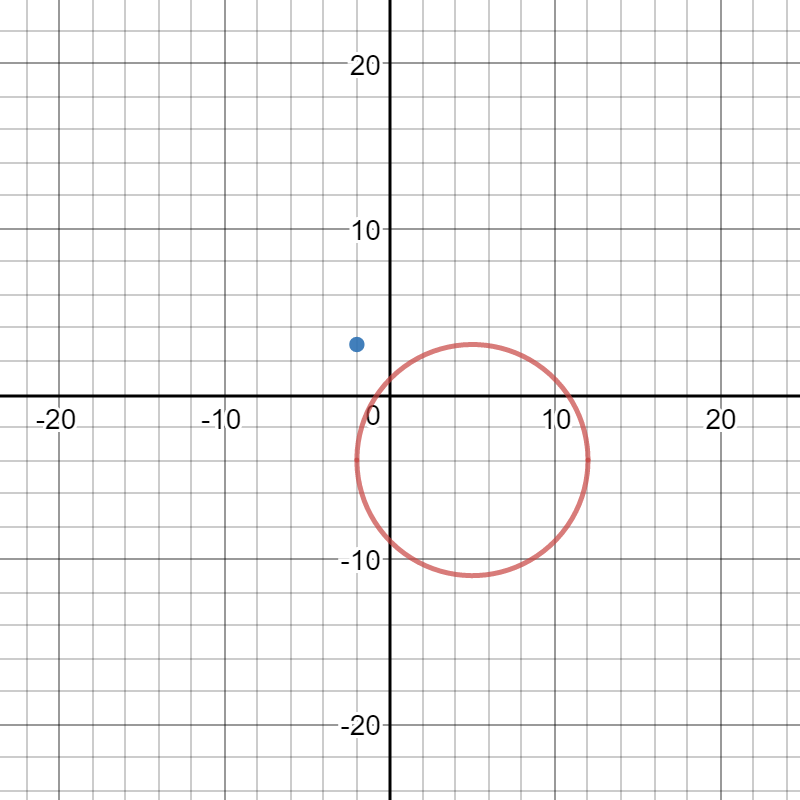
Please observe that the point does not lie on the circle.
We need to complete the squares so that we have the standard Cartesian form:
Combine the constant terms and mark as equation [1]:
The point-slope form of a line through the point
Distribute m and mark as equation [2]:
Substitute equation [2] into equation [1]:
Combine like terms within the second square:
Expand the squares
Combine like terms:
We want the values of m that make the above equation have only 1 corresponding value of x; the means that the discriminant must equal 0:
An obvious root is
This is the horizontal line:
By symmetry, the other slope must be undefined; implying the vertical line:
Let's confirm this graphically:
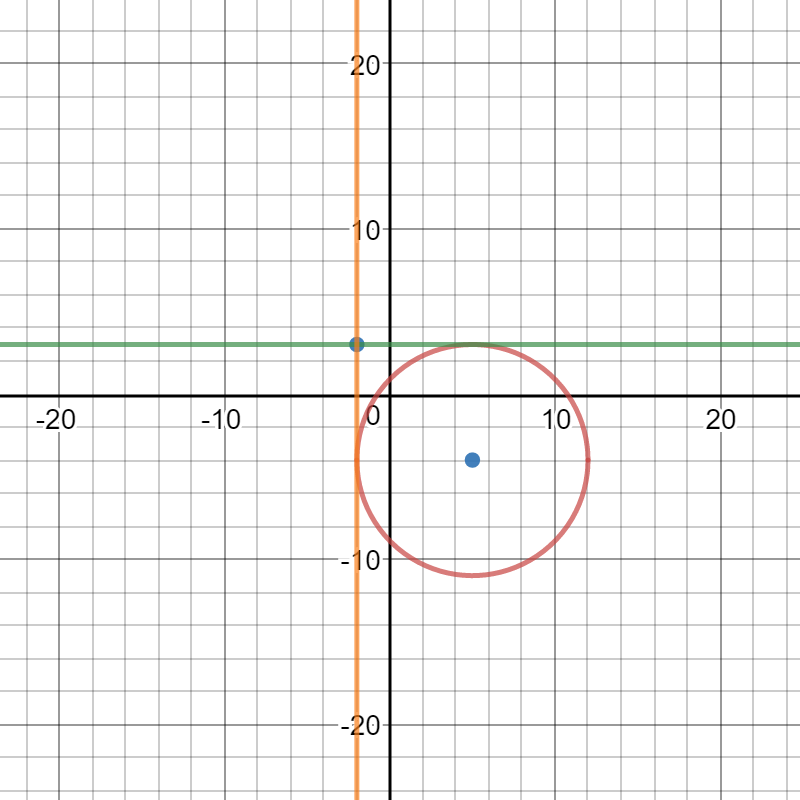
Confirmed! The equation of the tangent lines are:
NOTE: We could have obtained these answers by observing that the radius of the circle is 7 but this would have prevented me from showing you how to use
Explanation:
Let
rewriting it as
the Centre
For
This means that the point (pt.)
If
From Geometry we know that, the
centre to the tgt. equals the radius.
But, the
Hence,
But we surely know that there are
So, which can be the other tgt.?
Recall that, we have supposed that the slope of tgt. is
In other words, this means that we have taken it for granted
that the slope of tgt. exists.
Evidently, the other tgt. (which definitely exists ), must have the
undefined slope, i.e., must be the vertical line through
Clearly, this other tgt. is
It is easy to verify that the tgts.
Enjoy Maths.!
See below.
Explanation:
Using vectors.
Given a point
we can trace two tangent lines to
Let
or squaring
and then
but the tangency needs
now putting
and solving for
gives
NOTE:
Choosing

