Question

How do you find the Taylor polynomial Tn(x) for the function f at the number a `f(x)=sqrt(3+x^2)`, a=1, n=2?

Answer 1

`T_2(x) = (3x^2+2x+27)/16`

Explanation:

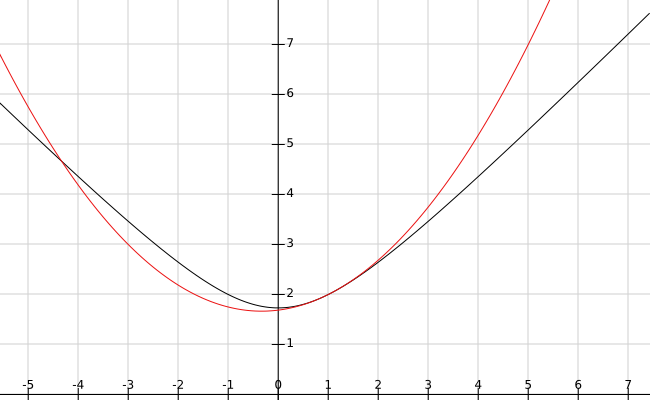
The Taylor polynomial of order `n` is the `(n+1)`-th partial sum of the Taylor series:

`f(x) = sum_(n=0)^oo (f^((n))(a))/(n!)(x-a)^n`

for `n=2` we have:

`d/dx sqrt(3+x^2) = x/sqrt(3+x^2)`

`d^2/dx^2 sqrt(3+x^2) = (sqrt(3+x^2) - x^2/sqrt(3+x^2))/(3+x^2) = 3/(3+x^2)^(3/2)`

So for `a=1`:

`f^((0))(1) = sqrt(3+1^2) = 2`

`f^((1))(1) = 1/sqrt(3+1^2) = 1/2`

`f^((2))(1) = 3/(3+1^2)^(3/2) = 3/8`

Then:

`T_2(x) = 2+1/2(x-1)+3/16(x-1)^2`

`T_2(x) = (32+8(x-1)+3(x-1)^2)/16`

`T_2(x) = (32+8x-8+3x^2-6x+3)/16`

`T_2(x) = (3x^2+2x+27)/16`