Question

How do you find the vertex, focus, and directrix of a hyperbola `(y-2)^2 - (x^2)/4 = 1`?

Answer 1

The vertices are at (`0,3`) and (`0,1`).
The foci are at (`0, 2-sqrt5`) and (`0, 2+sqrt5`).
The directrixes are at `y = -sqrt5/5` and `y = sqrt5/5`

Explanation:

The standard form of the equation for a hyperbola with a vertical transverse axis is

`(y-k)^2/a^2 - (x-h)^2/b^2 –= 1`

Your equation is

`(y-2)^2 –x^2/4 = 1` or

`(y-2)^2/1^2 –(x–0)^2/2^2 = 1`

So `a = 1`, `b = 2`, `k = 2`, and `h = 0`

Direction

The negative sign in front of the `x`-variables shows that the transverse axis is vertical.

Your graph will look like the one below.

(from www.shmoop.com)

Vertices

The coordinates of the vertices are (`h, k + a`) and (`h, k - a`).

So your hyperbola has vertices at (`0,3`) and (`0,1`)

Foci

The coordinates of the foci are (`h, k-c`) and (`h,k+c`), where

`c = sqrt(a^2 + b^2) = sqrt(1^2 +2^2) = sqrt(1 + 4) = sqrt5`

So the foci are at (`0, 2-sqrt5`) and (`0, 2+sqrt5`).

Directrixes

The equation for the directrixes is `y =k ± 1/c = 1± sqrt5`

`y = 2 - sqrt5/5`

`y = 2 + sqrt5/5`

Your hyperbola looks like this:

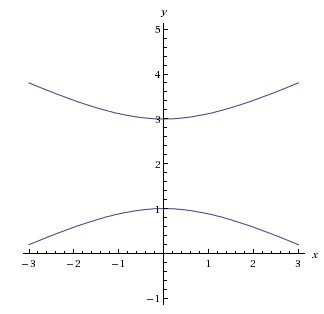
(generated by www.wolframalpha.com)