Question

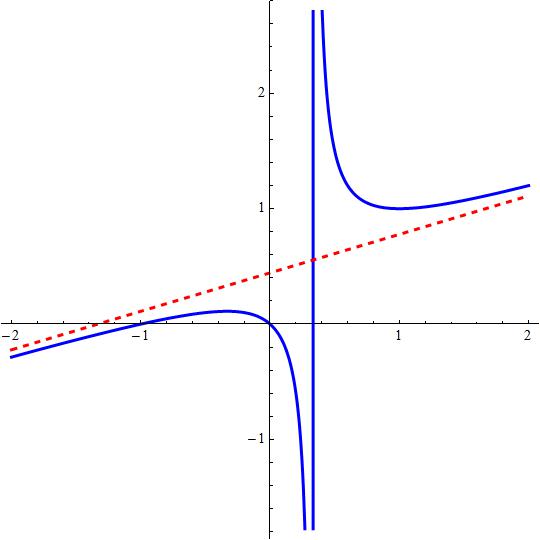
How do you find the Vertical, Horizontal, and Oblique Asymptote given `f(x)=(2x^3+3x^2+x)/(6x^2+x-1)`?

Answer 1

A vertical assymptote at `x = 1/3` and
a slant assymptote given by `y = x/3+4/9`

Explanation:

`f(x) = (2 x^3 + 3 x^2 + x)/(6 x^2 + x - 1) = 1/3(x (x+1/2)(x+1))/((x-1/3)(x+1/2)) = 1/3(x(x+1))/((x-1/3))`

We have a vertical assymptote at `x = 1/3` and also we know

`1/3x(x+1) = (x-1/3)(ax+b)+c`

Equating power coefficients

#{ (b/3 - c=0), ( 1/3 + a/3 - b=0), (1/3 - a=0) :}#

and solving

`a = 1/3,b=4/9,c=4/27`

The assymptote is given by

`y = x/3+4/9`

Attached a figure with vertical and slant assymptotes