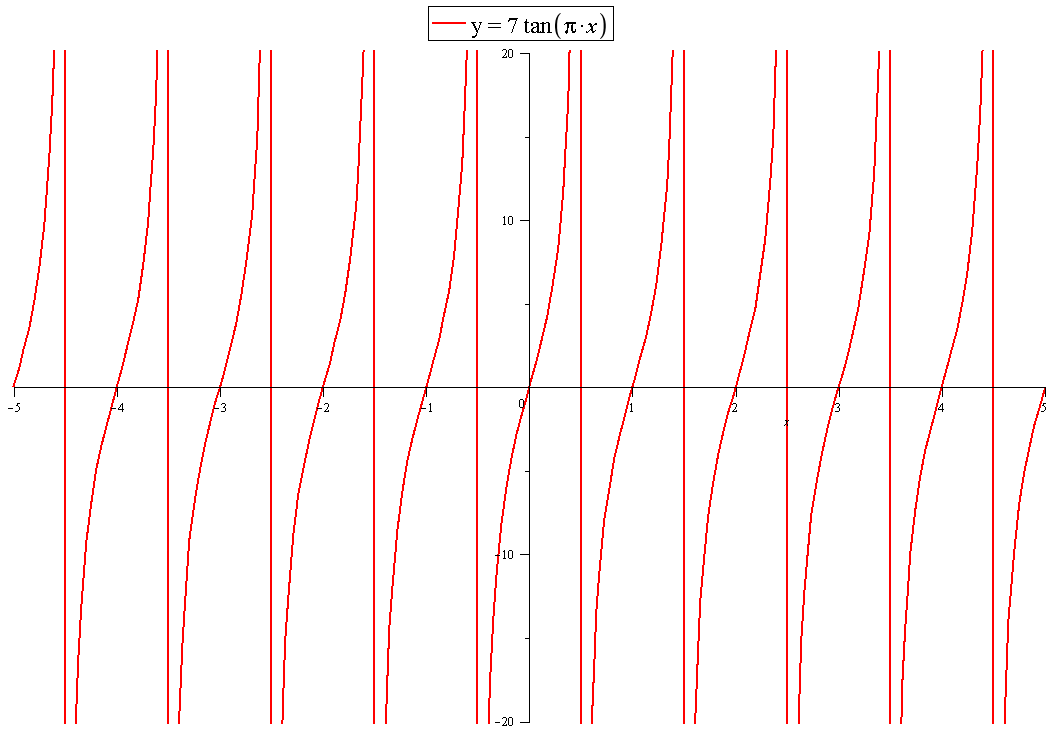
How do you find the Vertical, Horizontal, and Oblique Asymptote given #f(x) = 7 tan(πx)#?

1 Answer
Somebody N.
Apr 5, 2018

See below.

Explanation:

There are no oblique asymptotes. Oblique asymptotes occur in rational functions where the numerator is of higher degree then the denominator. This is not a rational function. The function is periodic, so no horizontal asymptotes.

Vertical asymptotes occur where the function is undefined.

#tanx# is undefined at #pi/2# , #pi+pi/2# etc.

We can express this as:

#npi+pi/2# where n is an integer.

#:.#

#y=7tan(pix)#

#pix=pi/2+npi#

#x=1/2+n#

so the function is undefined when #x=1/2+n#

#n in ZZ#

GRAPH:

enter image source here

Related questions
See all questions in Asymptotes
Impact of this question
1487 views around the world
You can reuse this answer
Creative Commons License