How do you find the vertical, horizontal and slant asymptotes of: #f(x)=(x^4-x^2)/(x(x-1)(x+2))#?
1 Answer
See below.
Explanation:
Start by simplifying the expression:
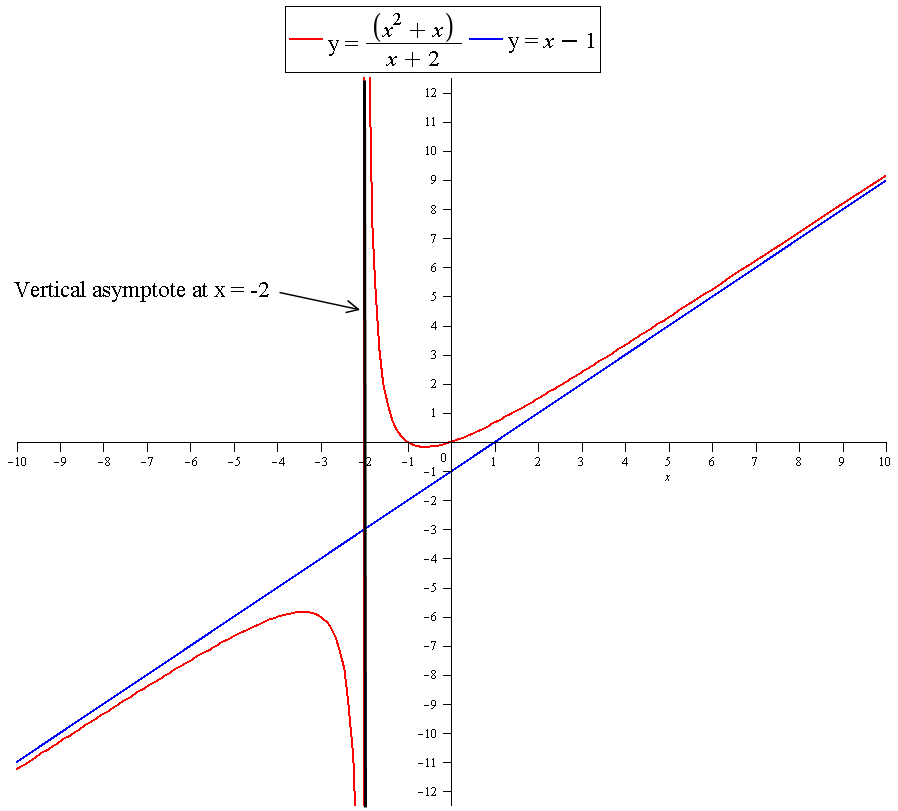
Vertical asymptotes occur where the function is undefined. This can be seen to be when
So the line
We now divide:
The quotient of this will be the oblique asymptote:
We do not need to be concerned with the remainder. So the oblique asymptote is the line:
This is the line
Graph: