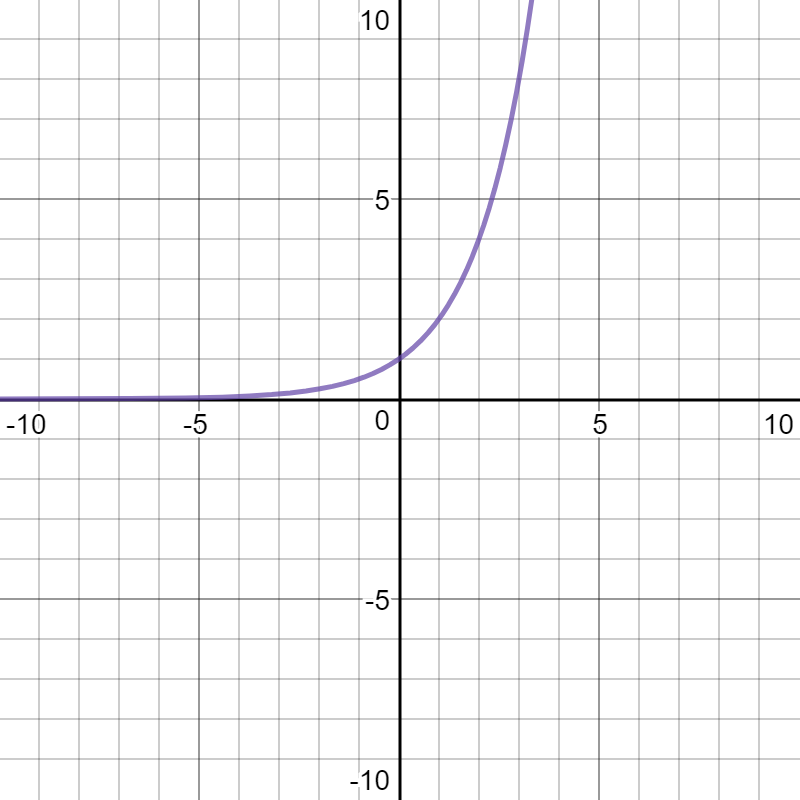
How do you find the vertical, horizontal and slant asymptotes of: #y= 2^x#?
1 Answer
Dec 18, 2017
This function has one asymptote at
Explanation:
Any function of the form
Exponential functions have infinite domains, because there is no number you can put in for
Since there are no
Note: You can also get the
Here's the graph: