How do you find the vertical, horizontal or slant asymptotes for #f(x) = (2x^2 + x + 2) /( x + 1)#?
2 Answers
Vertical asymptote at
No horizontal asymptote
Slant asymptote:
Explanation:
Given:
giving us the vertical asymptote of
and
so there is no horizontal asymptote.
Since the degree of the numerator is greater than the degree of the denominator,
we can divide the denominator into the numerator to get a slant asysmptote:
So the slant asymptote is
Slant Asymptote:
Vertical Asymptote:
Horizontal Asymptote: None
Explanation:
The given function is
To find the slant asymptote, divide numerator by the denominator of the given rational function.
The result of the division is
The whole number part of the quotient which is
which is the
To solve for the Vertical Asymptote, use the divisor and equate to zero
and the Vertical Asymptote is
There is
Kindly see the graph of the function
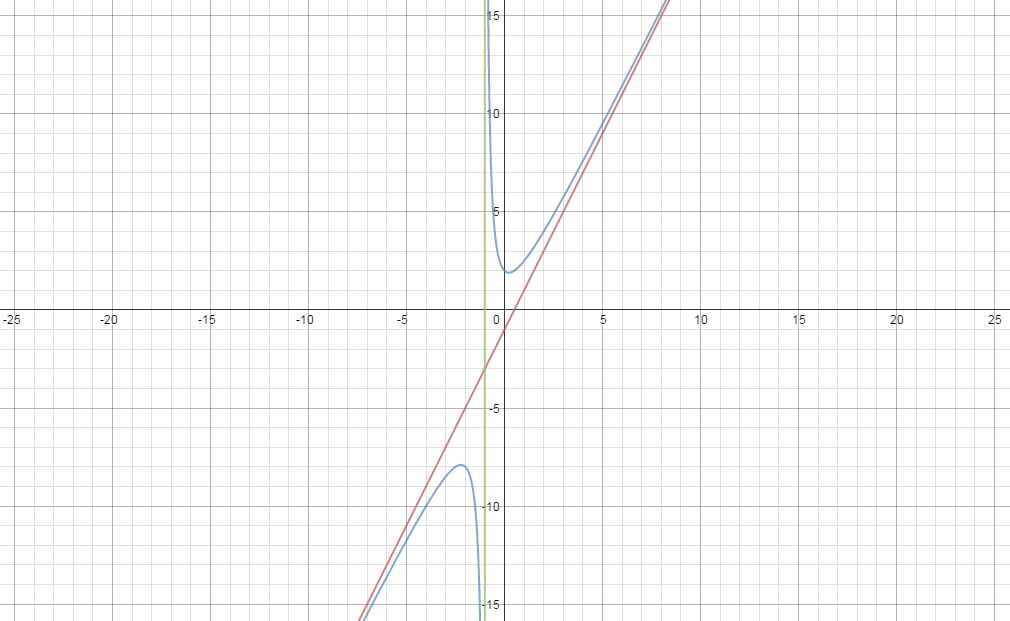
God bless....I hope the explanation is useful.
