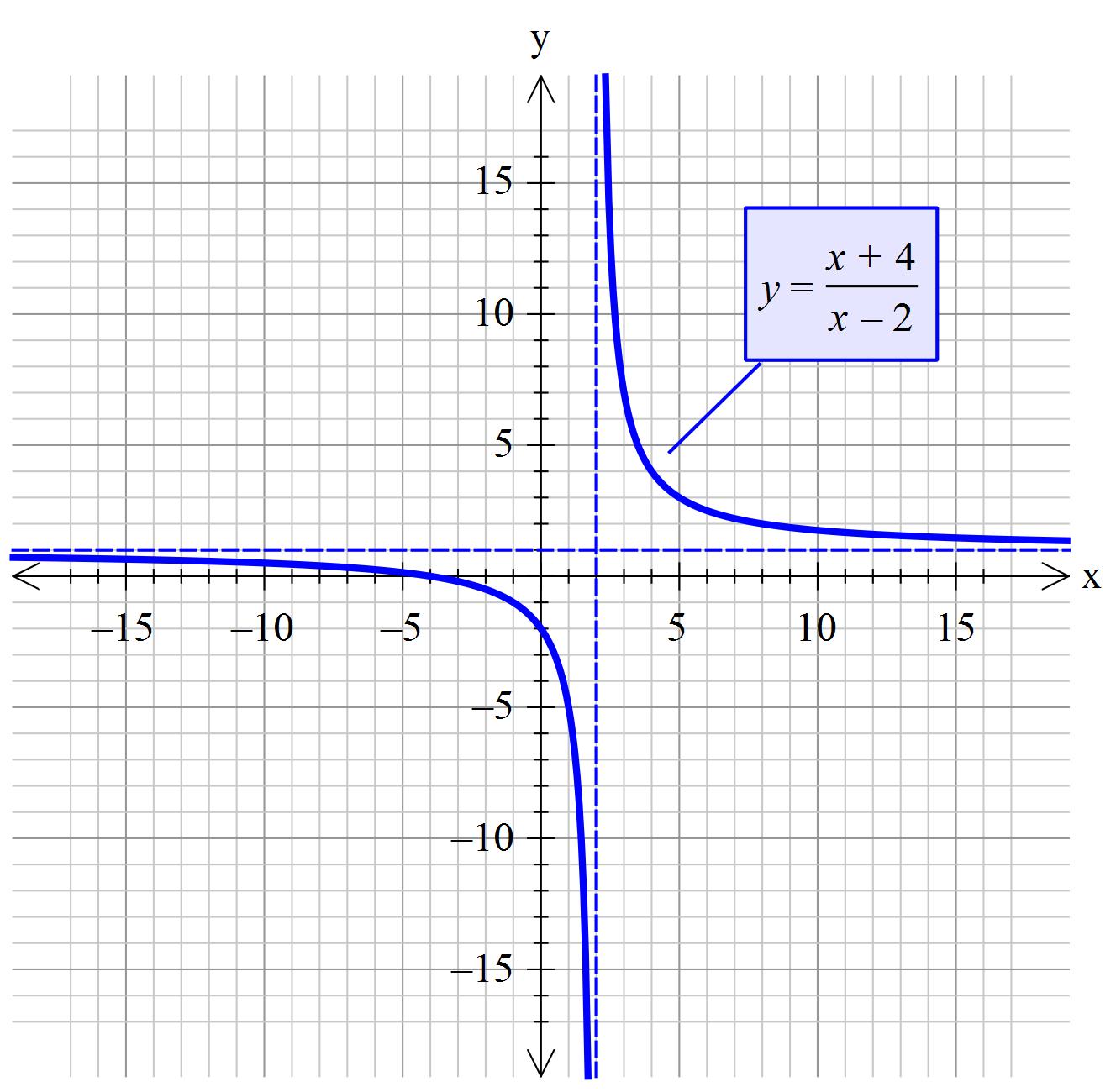
How do you find the vertical, horizontal or slant asymptotes for # f(x) = (x+4)/(x-2) #?
1 Answer
Apr 12, 2016
Explanation:
The equation is undefined when the denominator becomes 0. Consequently the excluded value is
As the value of
Thus
So