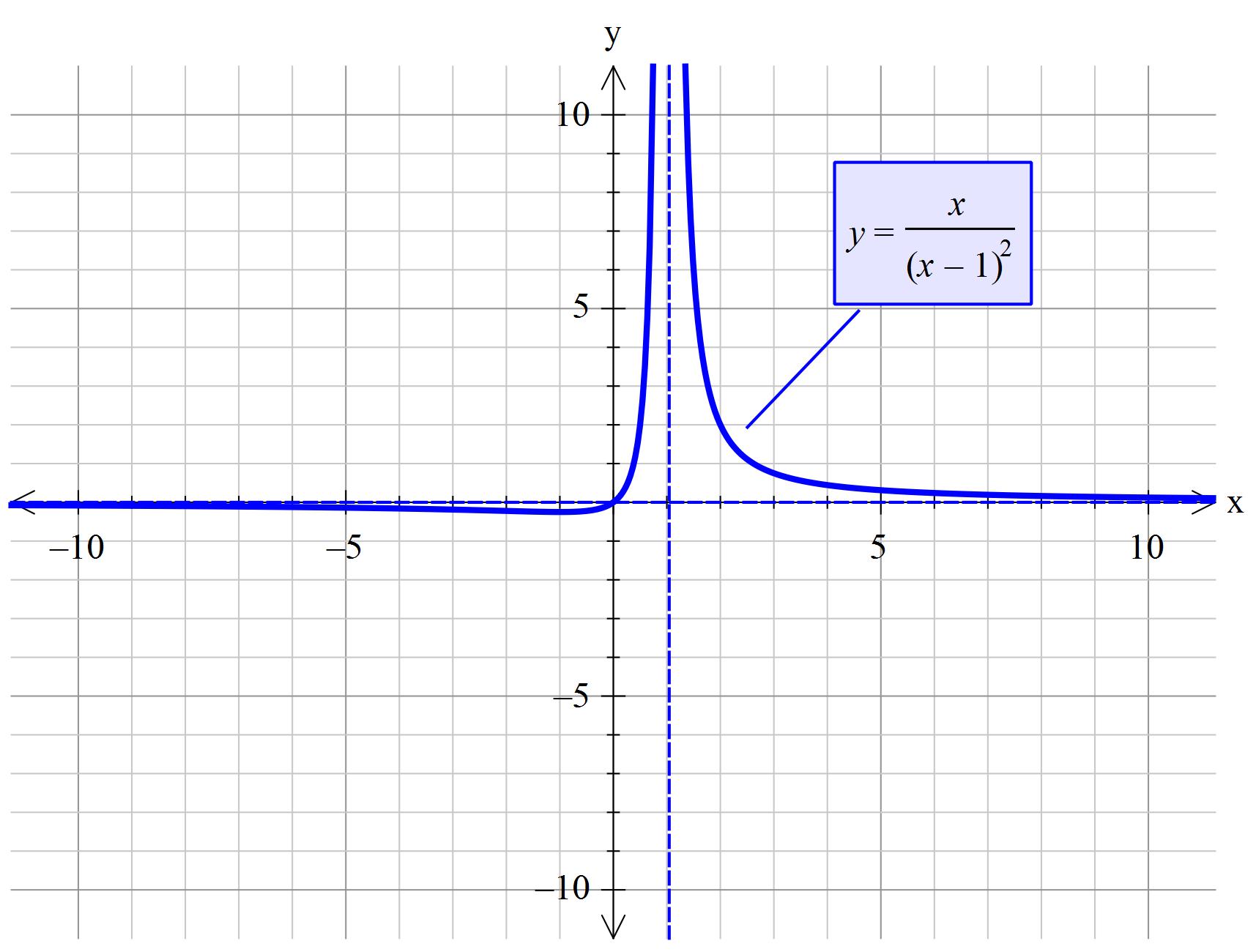
The basic rule is that you are 'not allowed' to divide by 0. Proper term for this is 'undefined'.
Given:#" "x/((x-1)^2)#
Expanding the brackets
#" " x/(x^2-2x+1)#
#color(blue)("Consider "x" becoming very large")#
As #x# becomes significantly large enough then the constants in the above equation become more and more insignificant. So there is a tendency for it to become:
#" " (cancel(x))/(cancel(x)(x-2))# which again has another constant.
So as it becomes bigger still there is a tendency for it to approach #1/x#
#lim_(xto-oo) 1/x= 0color(white)()^-#
#lim_(xto+oo) 1/x= 0color(white)()^+#
Thus #color(blue)(y=0" is an asymptote")#
'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
#color(blue)("Consider the case of the denominator "=0)#
#(x-1)^2=0 " "# is undefined
So #(x-1)=0 # is undefined
Thus #color(blue)(x=1" is an asymptote")#
'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~