How do you find the volume bounded by x = 1, x = 2, y = 0, and #y = x^2 # revolved about the x-axis?

Question

20664 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2017-11-29T06:28:53

Volume bounded by #x=1#, #x=2#, #y=0# and #y=x^2# is #(31pi)/5# units.

The area bounded by #x=1#, #x=2#, #y=0# and #y=x^2# is shown below (shaded in grey(

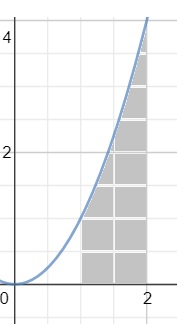
enter image source here

As it revolves around #x#-axis, its volume is given by

#int_1^2(piy^2)dx#

= #int_1^2(pi(x^2)^2)dx#

= #piint_1^2x^4dx#

= #pi[x^5/5]_1^2#

= #pi(2^5/5-1^5/5)#

= #pixx31/5#

= #(31pi)/5#