How do you find the volume of the region enclosed by the curves #y=2x#, #y=x#, and #y=4# is revolved about the y-axis?
1 Answer
Oct 21, 2015
Volume
Explanation:
The region described is the difference between two inverted cones as can be seen from the diagram below:
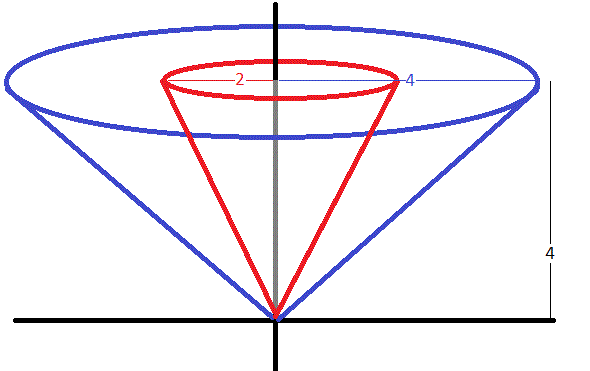
The volume of the bounded region is the difference between the volume of the external cone and the internal cone.
The general formula for the volume of a cone is
So the required region has a volume of
