Question

How do you find the volume of the region enclosed by the curves `y=x`, `y=-x`, and `x=1` rotated about the y axis?

Answer 1

If rotating about the y-axis, the shell method is your best bet to a quick solution.

Explanation:

`Volume=2piint_0^1x[x-(-x)]dx=2piint_0^1(2x^2)dx`

`=4/3pi`

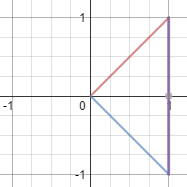
hope that helped

Answer 2

Look at the big picture then break it apart into extrusions.

Explanation:

https://www.desmos.com/calculator/zem7gewjxm

I see it like a (Cylinder-2Cone) instead of a funky shape. So if we find the volume of the cylinder we get `2pi` because `pir^2h`.

Now we have 2 Cones which are `pir^2h/3` which turns out to be `pi/3` because the height is now one. Now we take `2pi`-`2(pi/3)` or a total `V=(4pi)/3`