How do you find the volume of the solid bounded by the coordinate planes and the plane #8x + 6y + z = 6#?

Question

35470 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2016-07-10T17:29:12

#3/4#

use double integral (or triple if you like, i'll just do double as triple here is just extra unnecessary formality)

first we need to find the volume in question.

#8x + 6y + z = 6#

it hits the x,y,z axes as follows

#y,z = 0, x = 3/4#

#x,z = 0, y = 1#

#x,y = 0, z = 6#

so we can start with a drawing!!

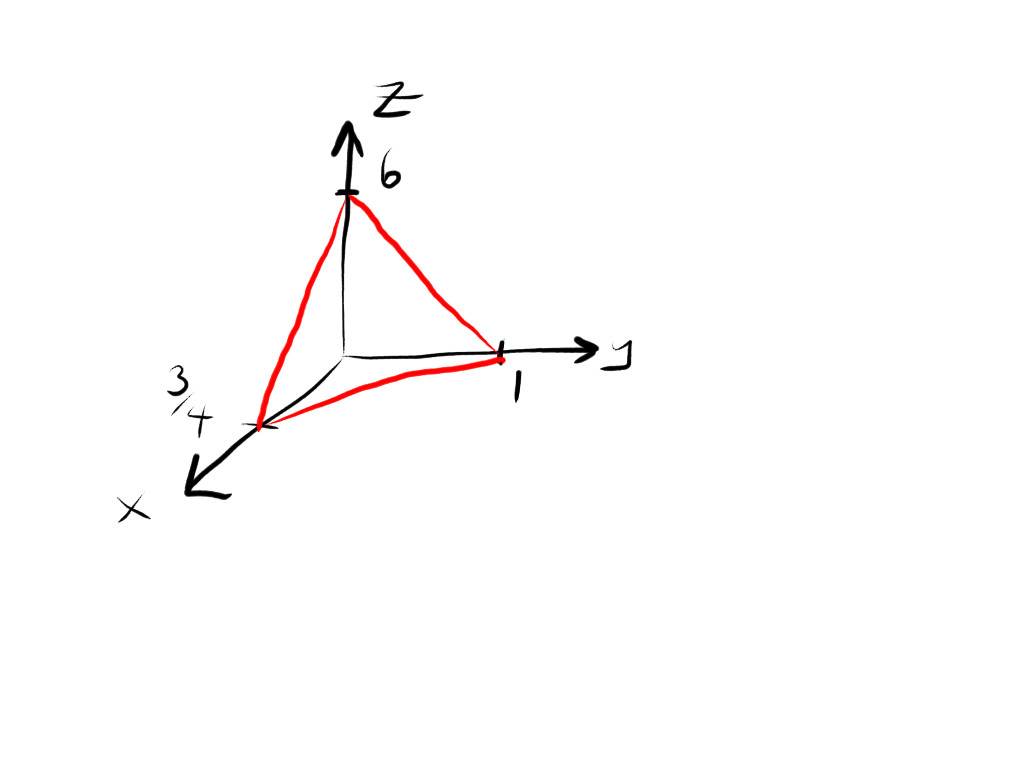
enter image source here

so it's just a case now of finding the integration limits for this double integral #int int \ z(x,y) dA = int int \ 6 - 8x - 6y \ dx \ dy#

in the x-y plane we have

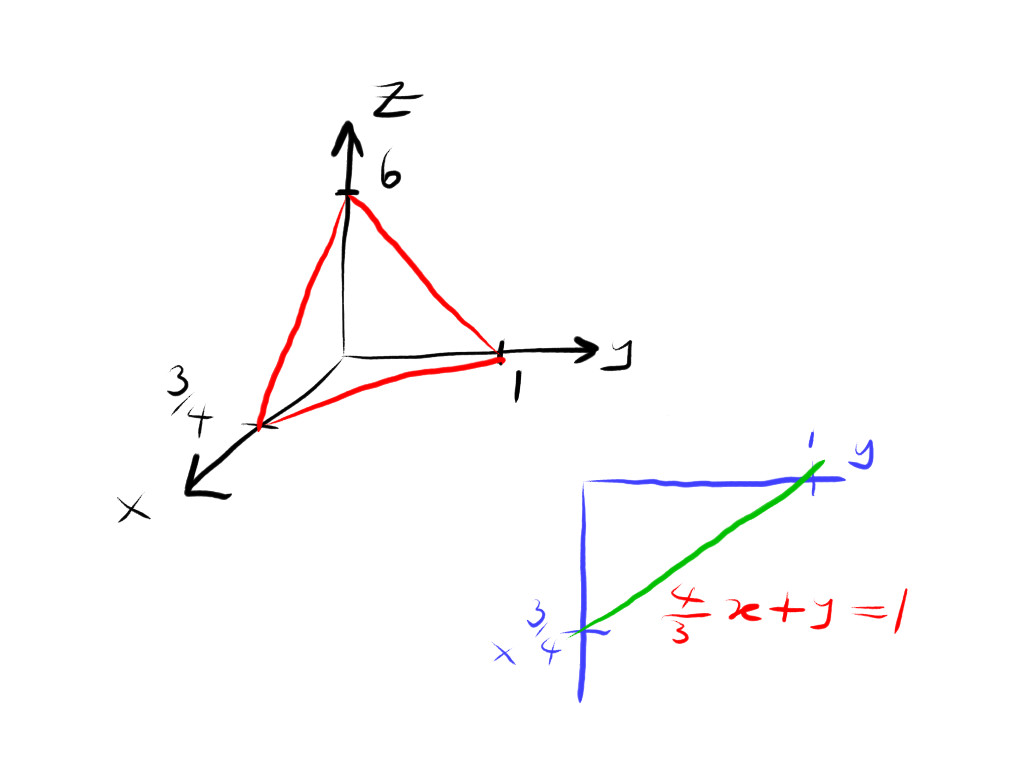
enter image source here

so either of these is fine

# int_{y=0}^{1} int_{x=0}^{3/4 (1-y)} \ 6 - 8x - 6y \ dx \ dy#

# int_{x=0}^{3/4} int_{y=0}^{1 - 4/3 x} \ 6 - 8x - 6y \ dy \ dx#

Either way, I get answer 3/4