Question

How do you find the volume of the solid whose base is the region bounded by y = x^2, y =x, x = 2 and x = 3, where cross-sections perpendicular to the x-axis are squares?

Answer 1

`=481/30`

Explanation:

Here's my go at a drawing, you may even get the idea from it.

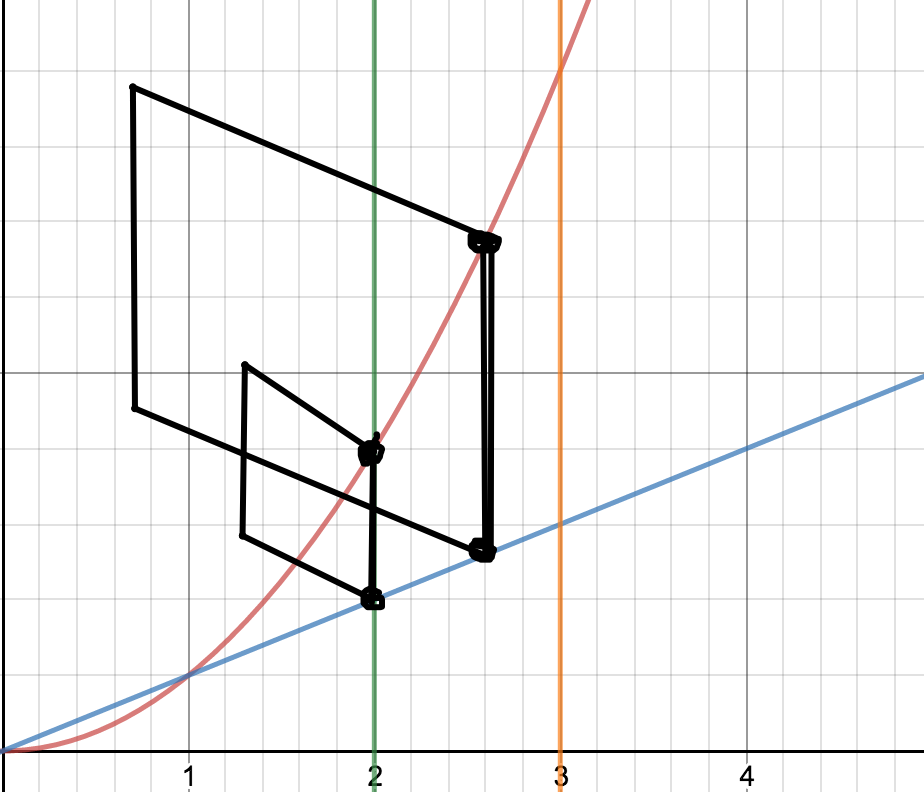
To clarify if not, the black squares are the cross sections of the solid, they are based on the xy plane and rise vertically to form these square cross sections.

At a given value of `x`, a square will have cross section area:

`A(x) = (y_2 - y_1) cdot (y_2 - y_1)` where:

`y_2 = x^2`

`y_1 = x`

So the volume, `V`, we are looking for is:

`V = int_2^3 A(x) \ dx`

`= int_2^3 (x^2 - x)^2 \ dx`

Easiest now is to expand integrand and use the power rule, term by term. It evaluates as:

`=481/30`