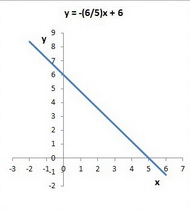
How do you find the x and y intercept and slope of #y= - 6/5x + 6#?
1 Answer
Jul 10, 2015
The slope is
Explanation:
The "slope-intercept" form of a straight line equation is
where
Your equation is
If we compare the two equations, we see that
So the slope is
To get the
The