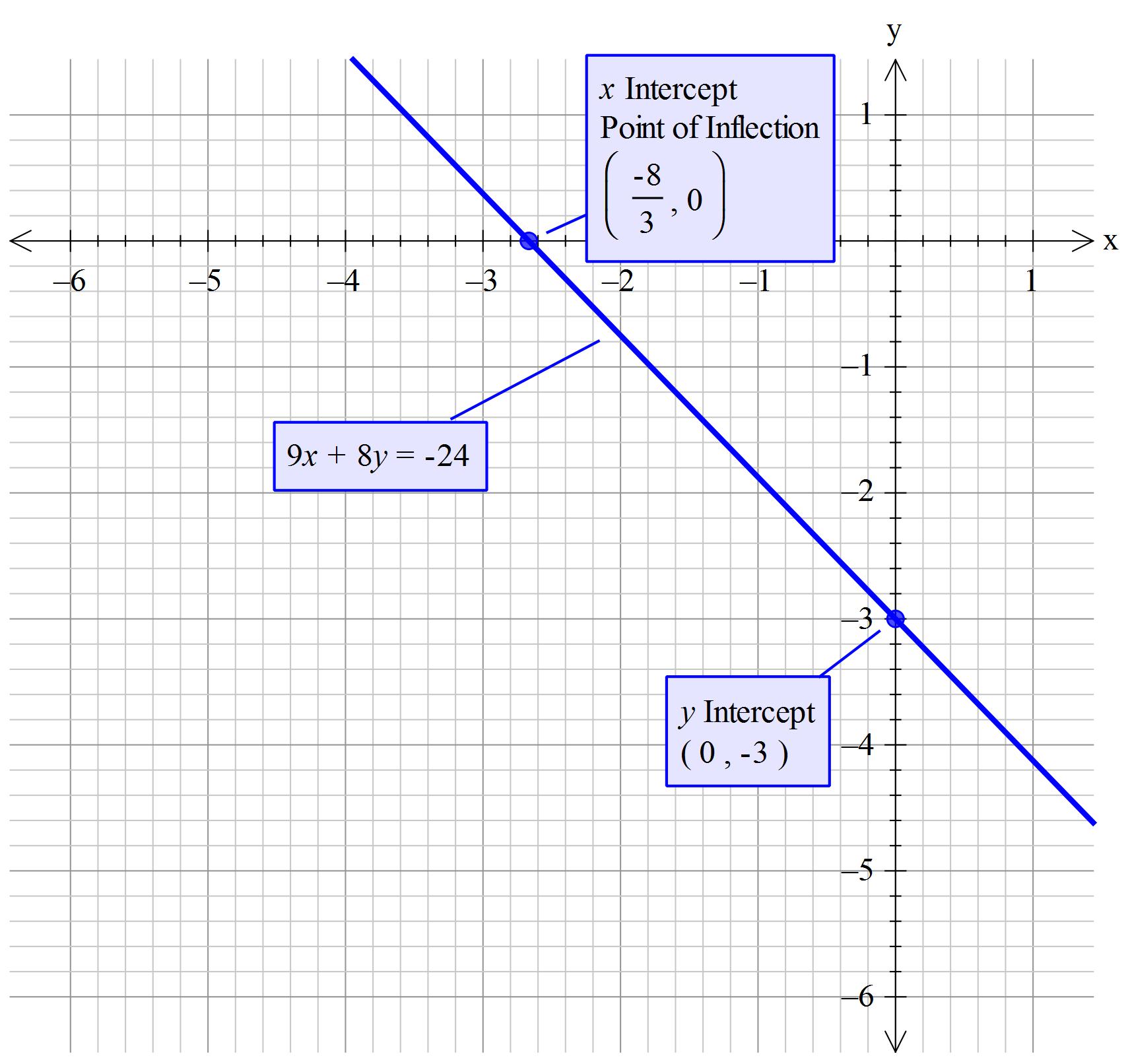
Convert the formula into the standard form of #y=mx+c# for a straight line graph.
Subtract #color(blue)(9x)# from both sides
#color(brown)(9xcolor(blue)(-9x)+8y=-24color(blue)(-9x))#
#8y=-9x-24#
Divide both sides by #color(blue)(8)#
#color(brown)(8/(color(blue)(8))xxy=-9/(color(blue)(8))x-24/(color(blue)(8)))#
But #8/8=1" and "24/8 =3# giving
#y=-9/8x-3#
,~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
#color(blue)("Determine y intercept")#
The line crosses the y-axis at #x=0# so by substitution
#color(brown)(y=-9/8x-3)color(blue)(" "->" "y=-9/8(0)-3#
#y_("intercept") = -3#
'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
#color(blue)("Determine x intercept")#
The line crosses the x-axis at #y=0# so by substitution
#color(brown)(y=-9/8x-3)color(blue)(" "->" "0=-9/8x-3#
#9/8x=-3#
#x=cancel((-3))^(-1)xx8/(cancel(9)^3)" " =" "- 8/3" " =" " -2 2/3#
#x_("intercept") = - 8/3#
'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~