Question

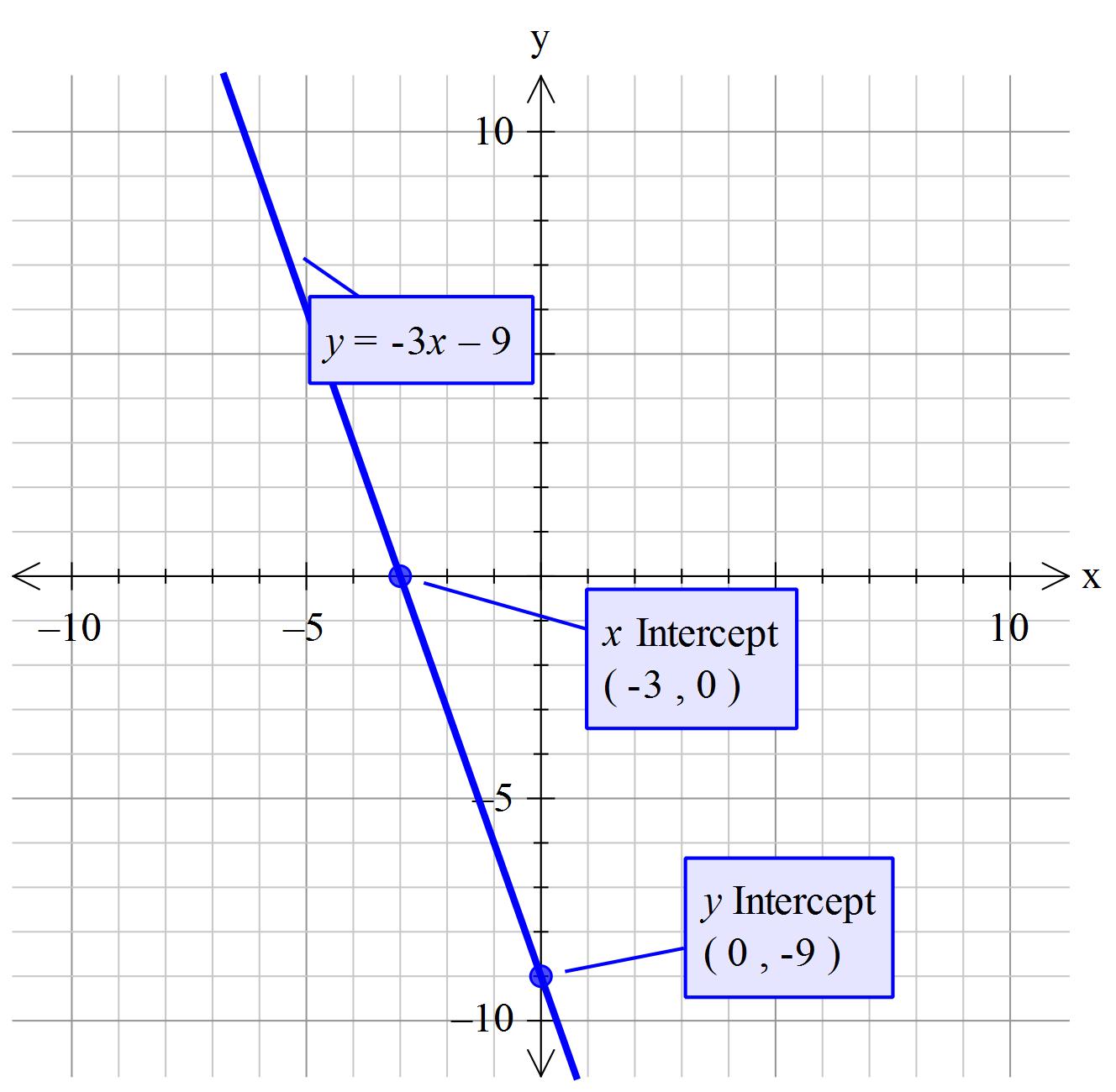
How do you find the x and y intercepts for `y= -3x-9`?

Answer 1

the x-intercept `=(-3, 0)`
the y-intercept `=(0, -9)`

Explanation:

To solve for the x-intercept, set `y=0` then solve for x

`y=-3x-9`
`0=-3x-9`
`3x=-9`

`x=-3` when `y=0`

therefore `(-3, 0)` is the x-intercept

To solve for the y-intercept, set `x=0` then solve for y

`y=-3x-9`
`y=-3(0)-9`
`y=-9` when `x=0`

therefore `(0, -9)` is the y-intercept

God bless....I hope the explanation is useful.

Answer 2

`y_("intercept")=-9->(x,y)->(0,-9)`

`x_("intercept")=-3->(x,y)->(-3,0)`

Explanation:

Reading directly from the equation:

`color(blue)(y_("intercept")=-9)`

The graph crosses the x-axis when y=0

Substituting `y=0` gives#

`0=-3x-9`

Add `color(blue)(9)` to both sides

`color(brown)(0color(blue)(+9)=-3x-9color(blue)(+9))`

`9=-3x+0`

Divide both sides by `color(blue)(3)`

`color(brown)(9/(color(blue)(3))=(-3)/(color(blue)(3))xx x)`

But `9/3=3" and "(-3)/3=-1`

`=>3=(-1)xx x`

`-x=3`

Multiply both sides by (-1)

`x=-3`

`color(blue)(x_("intercept")=-3)`
'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~