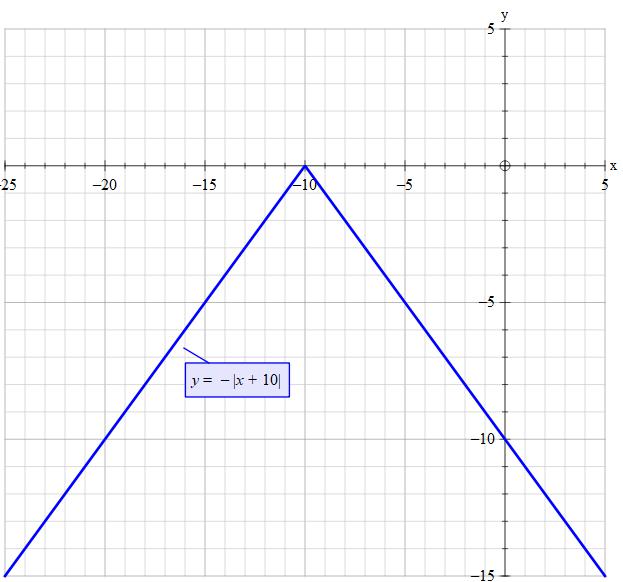
#color(blue)("Tip 1: Shape of the graph")#
If an absolute is positive we get the shape #vvv#
If an absolute is negative we get the shape #^^^color(red)( larr" Our one")#
This follows the same pattern as with a quadratic.
If the #x^2# term is positive we get #uuu#
If the #x^2# term is negative we get #nnn#
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
#color(blue)("Tip 2: horizontal position")#
If you add a value to the #x# then it moves the graph left
If you subtract a value from the #x# then it moves the graph right
Example: suppose we had say
#y=x^2+2x-2#
then we dicide to change it so that we add 4 to #x#. We have:
#y=(x+4)^2+2(x+4)-2#
Because we have added 4 it moves the graph #y=x^2_2x-2# left by 4
#color(red)("Our one:")#
So if we add 10 to #y=-|x|# giving #y=-|x+10|# we move the graph of #y=-|x|# left by 10
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
#color(blue)("Tip 3: x-intercept")#
The graph crosses the x-axis at #y=0#
#y=-|x+10| color(white)("d")-> color(white)("d") 0=-|x-10|#
The only way we can obtain 0 as the value of #y# is if #x=+10#
So we have: #x_("intercept")->(x,y)=(10,0)#
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
#color(blue)("Tip 4: y-intercept")#
The graph crosses the y-axis at #x=0#
#y=-|0+10| = -10#
So we have: #y_("intercept")->(x,y)=(0,-10)#
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
#color(blue)("Tip 4: The vertex")#
This occurs when the overall value #color(red)("within")# the absolute is about to 'flip' sign from positive to negative. That is, it becomes 0 which happens at #x=-10#
#y=-|color(magenta)(x)+10|#
#color(limegreen)(y)=-|ubrace(color(magenta)(-10)+10)| = color(limegreen)(0)#
#color(white)("ddddddddd")darr#
#color(white)("dddddddd.d")0#
Vertex #->(x,y)=(color(magenta)(-10),color(limegreen)(0))#