#y=x^5-2x^3#
To find points of inflection and changes in concavity, find the second derivative of #y#, which is #(d^2y) /( dx^2)#, and set it equal to zero.
#dy/dx = 5x^4 - 6x^2#
#(d^2y) /( dx^2) = 20x^3 - 12x#
Factor:
#(d^2y)/(dx^2) = 4(x)(5x^2-3)#
Set #(d^2y) /( dx^2)# equal to zero, and use the zero product rule to evaluate:
#0 = 4(x)(5x^2-3)#
#color(blue)(x = 0)#
#5x^2-3 = 0#
#5x^2 = 3#
#x^2 = 3/5#
#color(blue)( x= +- sqrt( 3/5 ))#
Draw a sign line for the signs of #(d^2 y)/(dx^2)#: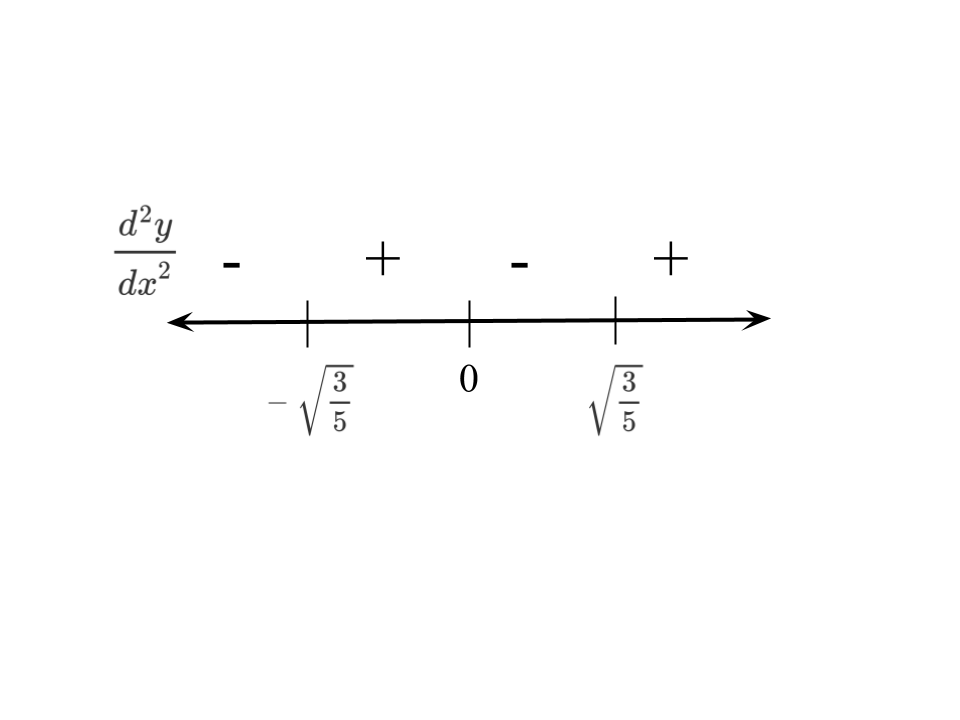
Therefore, #y# has points of inflection at #x=-sqrt(3/5), x=0, x=sqrt(3/5)#, #y# has no discontinuities, and is concave down for #x in (-oo,-sqrt(3/5)) uu (0, sqrt(3/5))#, and concave up for #x in (-sqrt(3/5),0) uu (sqrt(3/5),oo)#.


