Question

How do you find the zeros of `f(x) = 4x^5 + x^4 + x^3 + x^2 - 2x - 2`?

Answer 1

Numerically...

Explanation:

Given:

`f(x) = 4x^5+x^4+x^3+x^2-2x-2`

By the rational roots theorem, any rational zeros of `f(x)` are expressible in the form `p/q` for integers `p, q` with `p` a divisor of the constant term `-2` and `q` a divisor of the coefficient `4` of the leading term.

That means that the only possible rational zeros are:

`+-1/4, +-1/2, +-1, +-2`

None of these is a zero and hence we can tell that `f(x)` has no rational zeros.

Note that the signs of the coefficients are in the pattern `+ + + + - -`. With one change of sign, Descartes' Rule of Signs tells us that `f(x)` has exactly one positive real zero.

The signs of the coefficients of `f(-x)` are in the pattern `- + - + + -`. With `4` changes of signs, that means that `f(x)` has `4`, `2` or `0` negative real zeros.

In fact it has two complex conjugate pairs of non-real complex zeros.

Typically for a quintic polynomial none of these zeros is expressible in terms of `n`th roots or elementary functions. In theory they can be found using modular functions, but in practice it's probably better to stick with numerical approximations.

Using a Durand-Kerner method, I found approximate zeros:

`x_1 ~~ 0.854463`

`x_(2,3) ~~ 0.144877+-1.00403i`

`x_(4,5) ~~ -0.697109+-0.287521i`

Here's the C++ program I used:

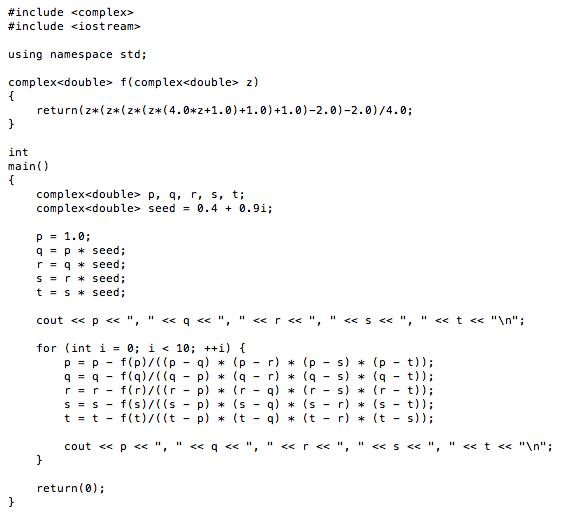
See https://socratic.org/s/aSVeQs9C for another example and a fuller description of this method.