How do you find the zeros of the polynomial function with equation # f(x) = -3(x+1/2)(x-4)^3#?
1 Answer
Aug 11, 2016
The zeors of
Explanation:
The zeros of
Since
either:
or:
This may be easier to visualise from the graph of
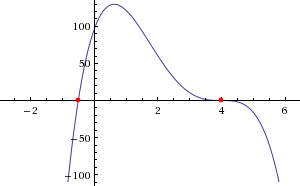
For interest:
