Question

How do you find the zeros of the polynomial function with equation `f(x) = x^3 +7x^2 - 4x - 28`?

Answer 1

Using the Factor Theorem (hoping or integer factors) we find zeros at `x in {-2,+2,-7}`

Explanation:

According to the Factor Theorem if `color(blue)(1)x^3+7x^2-4x-color(red)(28)` as rational zeros
they must be factors of `color(red)(28)/color(blue)(1)`

The possible factors are therefore
`color(white)("XXX"){+-1,+-2,+-4,+-7,+-14+-28}`

Testing these factors:

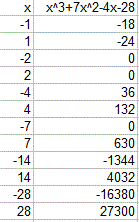
we find three zeros (as given in the "Answer" above.

Since the given expression is of degree 3 and we have 3 zeros, these 3 zeros represent all possible solutions.