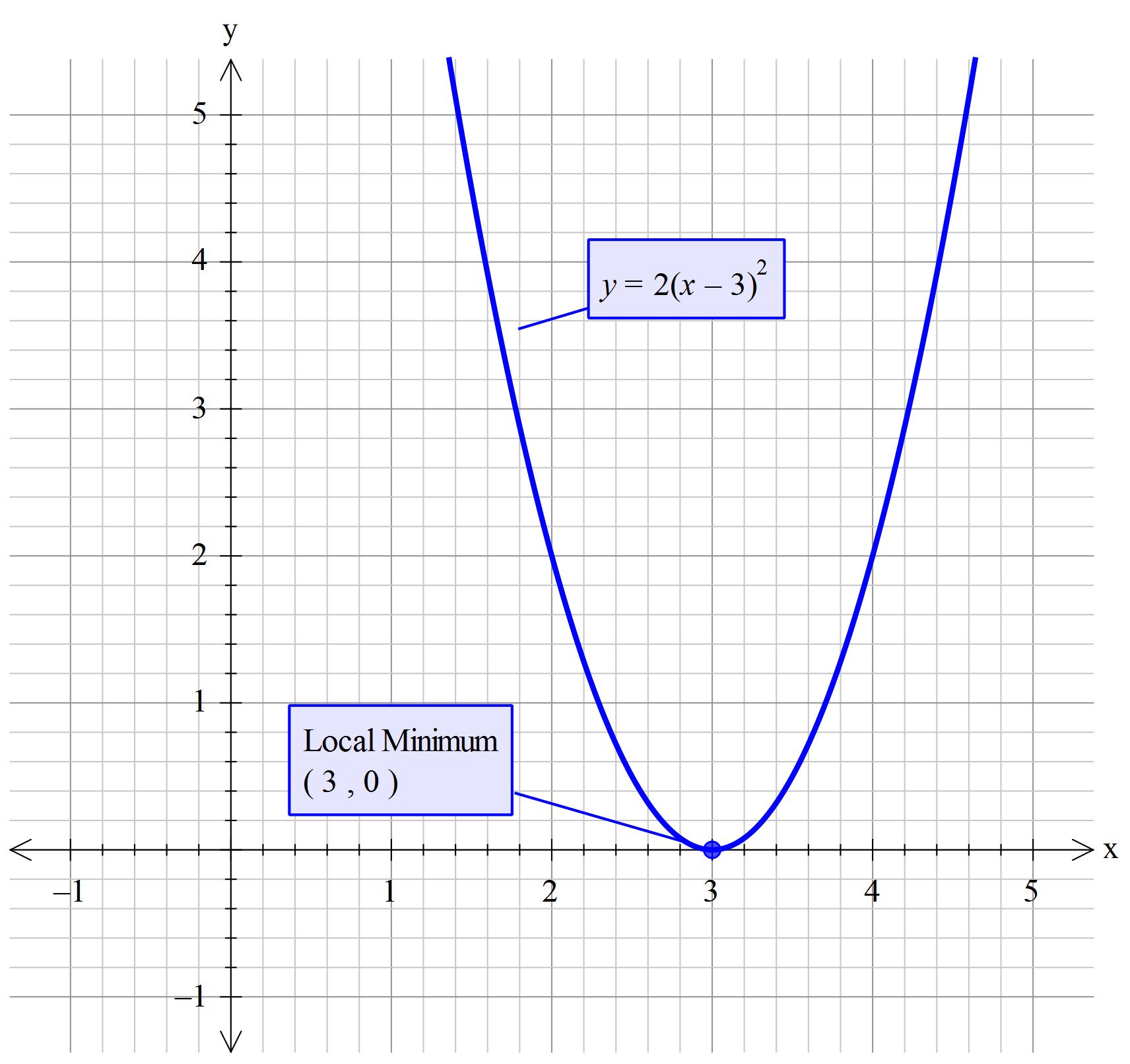
How do you find the zeros, real and imaginary, of # y=2(x-3)^2 # using the quadratic formula?

Question

1449 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2016-07-13T09:50:21

#x=3#

Squaring the bracket gives:

#y=2(x^2-6x+9)#

#y=2x^2-12x+18#
'...................................................
Using #y=ax^2+bx+c# where

#x=(-b+-sqrt(b^2-4ac))/(2a)#

#a=2"; "b=-12"; "c=18#
'........................................................

#x=(+12+-sqrt((-12)^2-4(2)(18)))/(2(2))#

#x=(+12+-sqrt(144-144))/4#

#x=+3" "# thus the x-axis is tangential to the vertex

Tony B