How do you find two solutions of the equations #costheta=-sqrt2/2#?
1 Answer
Sorry for the long answer, please read the explanation.
Explanation:
Assuming that you know the basics of the unit circle, if not memorized, you would know that there are two values for each sine, cosine, or tangent function, given that they are not the axis points.
So hypothetically,
These areas can be found simply by taking a glance at the unit circle or doing some mental work to force an image of it, if you memorized it, that is.
Take a look at this picture: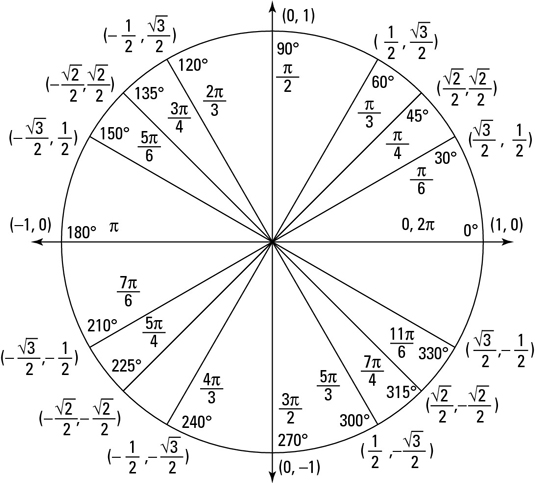
Sine cosine refers to and only to the
This proves that each unit circle value has another that shares the same cosine value, with the exception of axis values.
So to do a different question that is similar to this, simply take a look at a unit circle and find the value that corresponds. Since everything is in the same spot but in different quadrants, you will always find another value.
If you have not memorized the unit circle, I strongly suggest you watch the below video. It is a simple way to remember the unit circle and will save you lots of time in the future.
An easy method to memorize the unit circle, if you haven't already

