Question

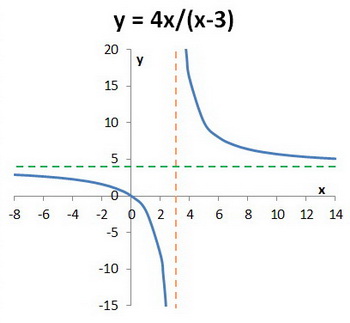
How do you find vertical and horizontal asymptotes of `(4x)/(x-3)`?

Answer 1

There is a vertical asymptote at `color(red)(x=3)` and a horizontal asymptote at `color(red)(y=4)`.

Explanation:

`f(x)=(4x)/(x-3)`

Step 1. Find the vertical asymptotes.

Set the denominator equal to zero and solve for `x`.

`x-3=0`

`x=3`

There is a vertical asymptote at `x=3`.

Step 3. Find the horizontal asymptotes.

Since the numerator and denominator are the same degree, we must divide the coefficients of the highest terms.

`4/1=4`

The horizontal asymptote is at `y=4`.