Question

How do you find vertical, horizontal and oblique asymptotes for `f(x)= x^(1/3)`?

Answer 1

Your function can be called the cube root function. Here is the graph: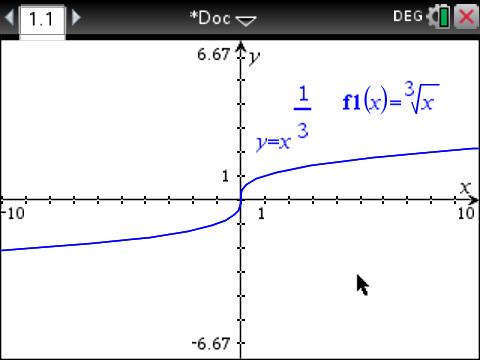

Explanation:

This function does not have any asymptotes. It has some nice rotational symmetry, because it is an "odd" function. It is the inverse of `f(x)=x^3` which means that its graph would be a reflection across the line y = x. If you wish to investigate asymptotes for functions, perhaps take a look at "Rational" functions.