Question

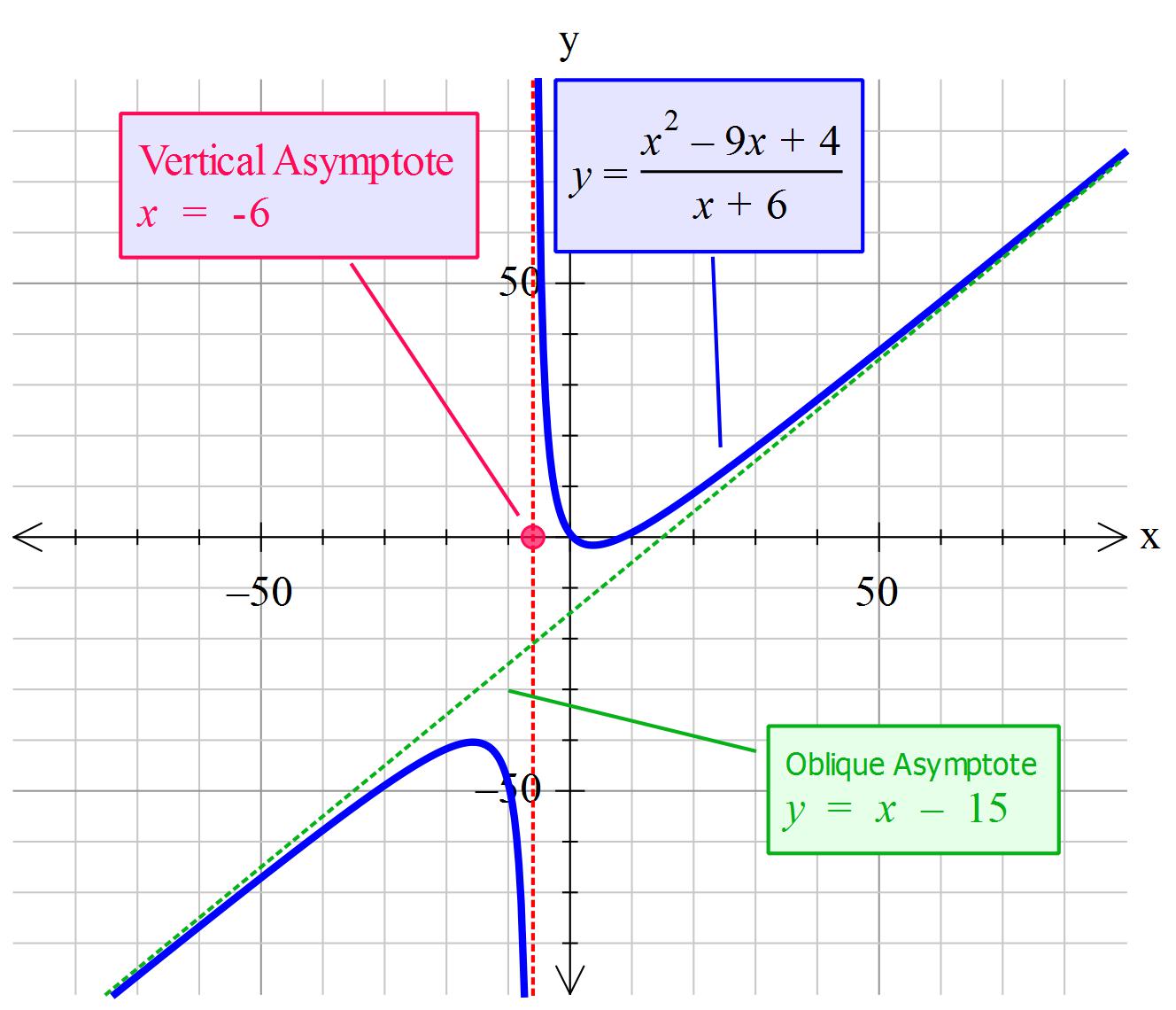
How do you find vertical, horizontal and oblique asymptotes for `(x^2-9x+4)/(x+6)`?

Answer 1

The vertical asymptote as at `" "x=-6`
The oblique asymptote is `" "y=x-15`

Explanation:

Given:`" "(x^2-9x+4)/(x+6)`

'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
`color(blue)("Determine the vertical asymptote")`

The equation is undefined at the denominator being 0

So the excluded value is that which gives `1+6= 0`

`color(green)("So the vertical asymptote as at "x=-6)`

'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

`color(blue)("Determine the oblique asymptote")`

Investigate the extreme values of `x`

`color(brown)("I can not spot how to simplify the given expression so by")`
`color(brown)("polynomial division we have "y= x-15+94/(x+6))`

`y=lim_(x->color(white)()^(-)oo ) x-15+94/(x+6)" "=" "x-15`

`color(green)("So the oblique asymptote is "y=x-15)`