Question

How do you find which quadrant each question is referring to if pi<a<3pi/2, 3pi/2<B<2pi?

Answer 1

While `pi < a < (3pi)/2` refers to `Q3`, `(3pi)/2 < B < 2pi` refers to `Q4`

Explanation:

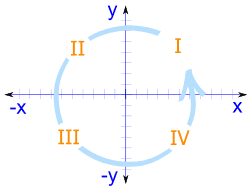
Cartesian plane is divided into four quadrants.

In first quadrant we have both abscissa and ordinates positive. In this quadrant, if we join the point to origin, the angle formed by this line with positive side of `x`-axis, say `theta` is between `0^@` and `90^@` or `pi/2` (in radians), which we can write as `0 < theta < pi/2`.

In second quadrant while abscissa is negative, ordinate is positive. In this quadrant, if we join the point to origin, the angle `theta` formed by this line with positive side of `x`-axis is between `90^@` and `180^@` or between `pi/2` and `pi`, which we can write as `pi/2 < theta < pi`.

In third quadrant while abscissa and ordinate both are negative. In this quadrant, if we join the point to origin, the angle `theta` formed by this line with positive side of `x`-axis is between `180^@` and `270^@` or between `pi` and `(3pi)/2`, which we can write as `pi < theta < (3pi)/2`.

In fourth quadrant while abscissa is positive, ordinate is negative. In this quadrant, if we join the point to origin, the angle `theta` formed by this line with positive side of `x`-axis is between `270^@` and `360^@` or between `(3pi)/2` and `2pi`, which we can write as `(3pi)/2 < theta < 2pi`.

Hence while `pi < a < (3pi)/2` refers to `Q3`, `(3pi)/2 < B < 2pi` refers to `Q4`