How do you graph #3x-y=7#?
2 Answers
Jul 22, 2017
Plot the points
Join these two points you will get the curve.
Explanation:
Given -
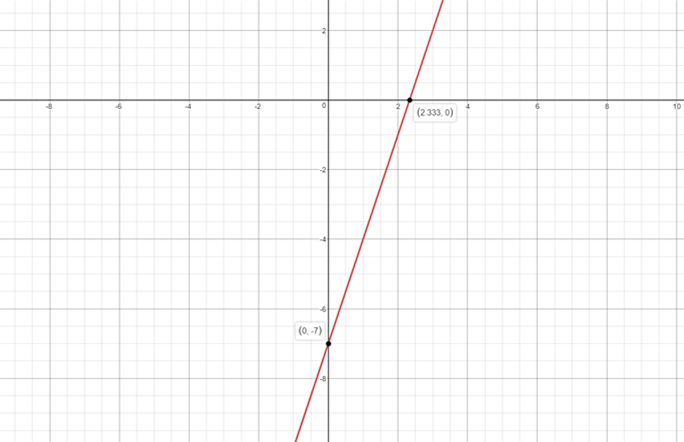
#3x-y=7#
Find the two intercepts. Plot them and
join them with a straight line.
x-intercept
At
#3x-0=7#
#x=7/3=3.3#
#(3.3,0)#
y-intercept
At
#3(0)-y=7#
#y=-7#
#(0,-7)#
Plot the points
Join these two points you will get the curve.
Jul 22, 2017
I would rearrange the equation into standard form:
This means that the line has a gradient (slope) of
Graph the function by drawing a line through the point
Explanation:
Subtract
Multiply both sides by
This means that the line has a gradient (slope) of

