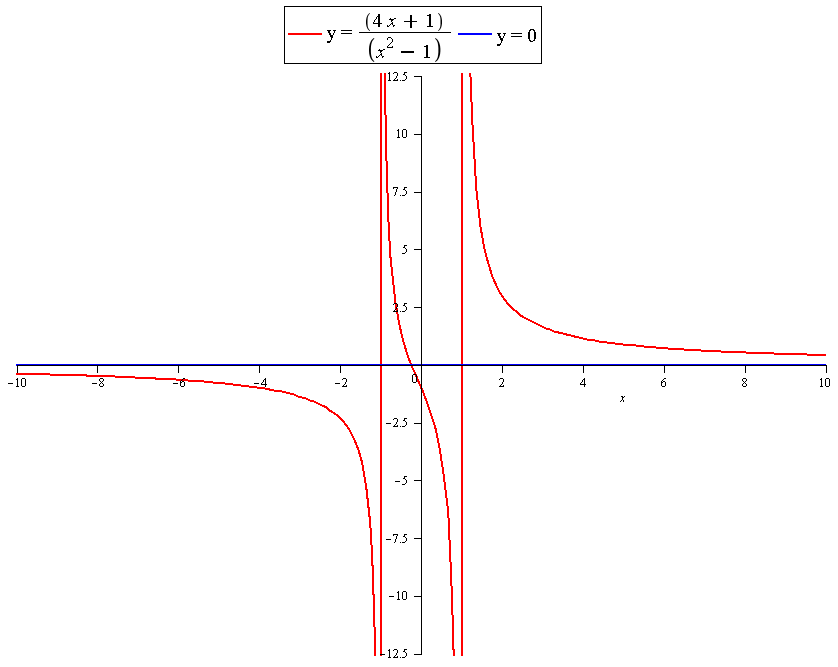
How do you graph #(4x+1)/(x^2-1# using asymptotes, intercepts, end behavior?

Question

1935 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2017-11-09T16:17:09

See below.

#(4x+1)/(x^2-1)# is undefined for #x=1 or -1# ( Division by zero )

So the line #x=1 and x=-1# are vertical asymptotes.

Y axis intercept occurs when #x =0#

#y=(4(0)+1)/((0)^2-1)=-1# ( 0 , -1 )

x axis intercepts occur when y = 0.

#(4x+1)/(x^2-1)=0#

We can solve this by reasoning that if #(4x+1)=0#

Then:

#(4x+1)/(x^2-1)=0#

#:.#

#(4x+1)=0 =>x=-1/4#

Note: Do not try to solve for #(x^2-1)=0# ( zero denominator is invalid )

x axis intercept at:

#(-1/4 , 0 ) #

For limits to infinity we only need to concern ourselves with the two terms containing the variable.

#(4x)/x^2#

#(4x)/x^2=4/x#

#lim_(x->oo)(4/x)=0#

#lim_(x->-oo)(4/x)=0#

So the x axis is a horizontal asymptote.

Graph:

enter image source here