Question

How do you graph `4x^2+4y^2-16x-16y+23=0`?

Answer 1

`(x-2)^2 /(9/4) +(y-2)^2/(9/4) = 1`

Center: `(2,2)`

`a= 3/2; b= 3/2 ; c = 0`

`e= 0`

Explanation:

First, complete the square to write the equation in standard form of an ellipse

The goal in completing the square to create perfect trinomial in either one of this form

`(a^2 + 2ab+ b^2) = (a+b)^2`

`(a^2 -2ab +b^2) = (a-b)^2`

Given `4x^2 + 4y^2 -16x -16y +23= 0`

Rewrite as follow: `(4x^2 -16x) + (4y^2 -16y) = -23`

`4(x^2 -4x) + 4(y^2 -4y) = -23`

`4(x^2 -4x + color(red)(4)) + 4(y^2 -4y + color(red)(4)) = -23 + color(red)(16 + 16)`

`4(x-2)^2 + 4(y-2)^2 = 9`

Divide both side by 9, to get the general form of an ellipse

`(4(x-2)^2)/9 +( 4(y-2)^2)/9 = 9/9`

`(x-2)^2 /(9/4) +(y-2)^2/(9/4) = 1`

Center: `(2, 2)`

`a^2 = 9/4 = a = 3/2`

`b^2 = 9/4 = b = 3/2`
`c^2 = a^2 - b^2 = 9/4 -9/4`

`c= 0`

Foci: `(2-0, 2) => (2,2)`

`(2-0, 0) => (2,2)`

Vertices: `(2-3/2 , 2) => (1/2 , 2)`

`(2 + 3/2 , 2) => (7/2 , 2)`

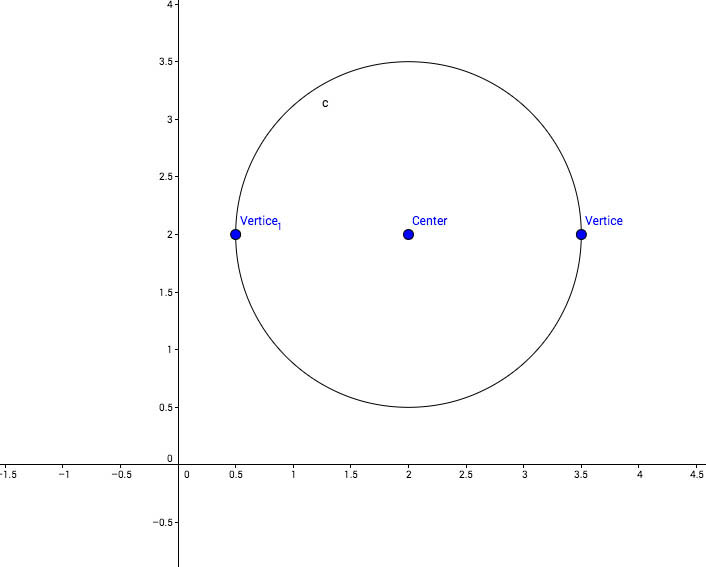
To graph, plot the center first.

Then from the center to left 1.5, right 1.5
Then from center go up 1.5 and down 1.5
Then connect those point as best as you can

This ellipse look like a circle because eccentricity is `e = c/a`

`e = 0/(3/2) = 0` , look like circle, more rounded.