How do you graph #4x^2+9y^2+24-18+9=0#?
1 Answer
(see below)
Explanation:
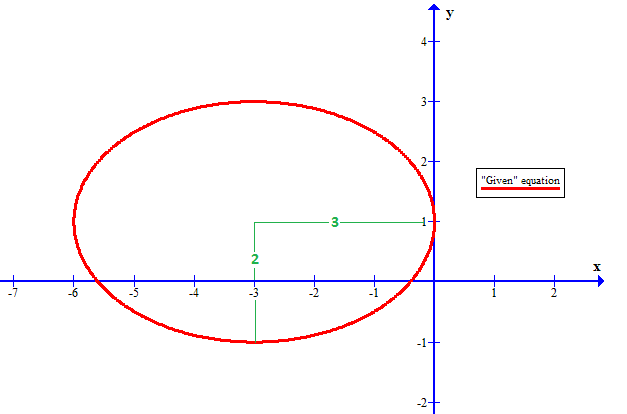
Note: I am assuming that the equation should have been:
The standard form of an ellipse is
with center at
radius on X-axis
radius on Y-axis
Converting the (assumed) equation into this form:
So we need to draw an ellipse with center at
a radius of
a radius of