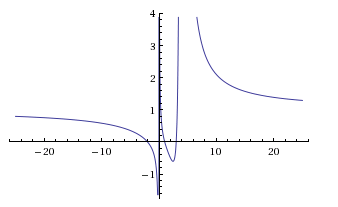
How do you graph and find the discontinuities of #H(x) = [(x - 1) (x + 2) (x - 3)]/(x(x - 4)^2#?
1 Answer
First we find every assymptote and root, and then start making a table of values. The discontinuities are the vertical assymptotes.
Explanation:
First thing we do, is look for any vertical assymptotes. Those are the values the function can never take, usually because it'll cause a math error (division by zero, logarithm of a number that's zero or negative, negative number in an even root, etc.)
In this case, the only things that can make things go wrong is the denominator. Just make the inequality, and solve it.
Since it's a product, either can't be zero, so
We have two vertical assymptotes, and they are
The horizontal or slant assymptotes are basically extremes. What happen when the value of x get infinitely big. We could just keep plugging bigger and bigger numbers until we see a pattern, or, we can pretend
Since
Basically, when
So we have a horiontal assymptote (since it's a horizontal line),
Now, since we have our suggestion's guidelines, all that's left is actually picking values and then connecting the dots. We know this function has 3 roots, that is, three points of the form
They're