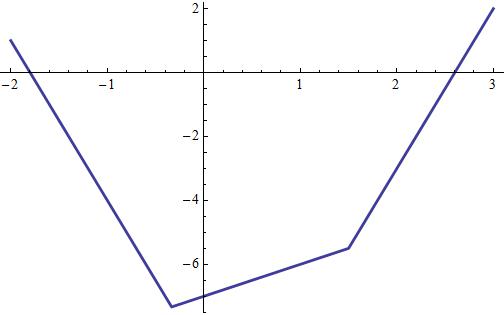
#abs(3x+1)+abs(2x-3)=11=3x+1-3x+10# so
#abs(3x+1)/(3x+1)+abs(2x-3)/(3x+1)=1+(10-3x)/(3x+1)# or
#pm1+abs(2x-3)/(3x+1)=1+(10-3x)/(3x+1)#
Now we have two options:
a)
#1+abs(2x-3)/(3x+1)=1+(10-3x)/(3x+1)->abs(2x-3)/(3x+1)=(10-3x)/(3x+1)#
b)
#-1+abs(2x-3)/(3x+1)=1+(10-3x)/(3x+1)->abs(2x-3)/(3x+1)=2+(10-3x)/(3x+1)#
Following with a) we have
a-1)
#abs(2x-3)=10-3x=2x-3-5x+13# or
#abs(2x-3)/(2x-3)=1+(13-5x)/(2x-3)# or
#pm1=1+(13-5x)/(2x-3)# with two options:
a-1-1)
#1=1+(13-5x)/(2x-3)->13-5x=0->color(red)(x=13/5)#
a-1-2)
#-1=1+(13-5x)/(2x-3)->0=2+(13-5x)/(2x-3)->color(red)(x=7)#
Now following with b)
#abs(2x-3)/(3x+1)=2+(10-3x)/(3x+1)->abs(2x-3)=6x+2+10-3x# so
#abs(2x-3)=3x+12# then
b-1)
#abs(2x-3)=2x-3+x+15->abs(2x-3)/(2x-3)=1+(x+15)/(2x-3)# or
#pm1=1+(x+15)/(2x-3)# with two options
b-1-1)
#1=1+(x+15)/(2x-3)->color(red)(x=-15)#
b-1-2)
#-1=1+(x+15)/(2x-3)->0=2+(x+15)/(2x-3)->color(red)(x=-9/5)#
After checking the found values, we pick the feasible values #x = -9/5# and #x = 13/5#