Question

How do you graph `f(x)=2/(x^2-4x+4)` using holes, vertical and horizontal asymptotes, x and y intercepts?

Answer 1

Hole: none
Vertical Asymptote: `x = 2`
Horizontal Asymptote: `y = 0`
x-intercept: none
y-intercept: `(0, 1/2)`

Explanation:

`f(x) = 2/(x^2-4x+4)`

First, let's factor this function. We can only factor the bottom, where we get `(x-2)^2`
(If you need help knowing how to factor, watch this video and start from 5:26:

So now our equation is: `f(x) = 2/(x-2)^2`

---

Hole : A hole literally means when there's a hole in the graph, like shown in this picture at the arrow:

To solve for holes, we need to see if any factors of the numerator (top) equal to the denominator (bottom). In our function, no value from the top equals to the bottom, so there are no holes.

I don't know how you want it to be written, but you can say " no holes" or "`cancel(0)`".

---

Vertical Asymptote: A (usually dotted) vertical line telling us that we cannot have any points touching that line.
To find the vertical asymptote, we set the denominator of the function equal to `0` and solve, like this:
`(x-2)^2 = 0`
`(x-2) = 0`
So our vertical asymptote is x = 2 (it's a line)
We usually graph asymptotes as dotted lines.

---

Horizontal Asymptote : There are a few rules for finding horizontal asymptotes.
So in the following, m = degree of the highest x-value in numerator
(ex: `x^2`, `x^5` and n = degree of highest x-value in denominator.)

If m > n (degree of x on top is greater than degree of x on bottom), then there is no horizontal asymptote.

If m = n (degree of x on top = degree of x on bottom), then you divide the leading coefficients of the numerator and denominator.

If m < n (degree of x on top is less than degree of x on bottom), then the horizontal asymptote is y = 0.

In our example, `2/(x-2)^2`, we can see that the numerator does not have an x value, but the bottom does. So in this case, m < n, meaning that the horizontal asymptote is y = 0 .

Again, we usually graph asymptotes as dotted lines.

---

x-intercept(s) : The x-intercept is what you get when you set the numerator to 0. In this case, since the numerator is `2`, there is no x-intercept.

---

y-intercept(s) : y-intercepts are what you get when you set x = 0.

When we plug into the equation `0` for all the x-values:
`f(x) = 2/(x-2)^2`
`f(x) = 2/(0-2)^2`
`f(x) = 2/(-2)^2`
`f(x) = 2/4`
`f(x) = 1/2`

So the y-intercept is `(0, 1/2)`.

Here is the graph of the function (the graph grows infinitely high/low and left/right). As you can see, the vertical asymptote is at 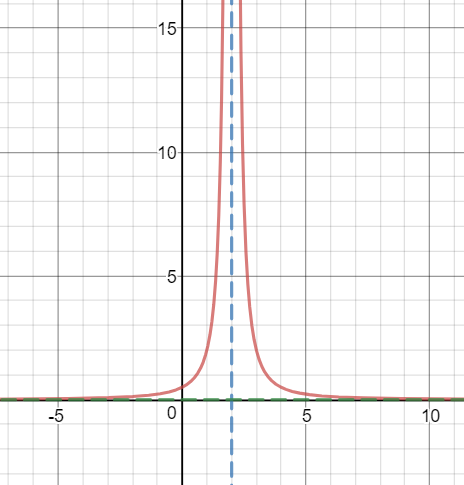`x = 2`, the horizontal asymptote is at `y = 0` (so the graph never touches the x-axis), there are no x-intercepts, and the y-intercept is `(0, 1/2)`.

Hope this helps! (Sorry I know this is long)