How do you graph #f(x)=2cosx-(sqrt2)# and solve over the interval [0,2pi)?
1 Answer
Feb 13, 2015
The graph of
is simply the graph of
(where
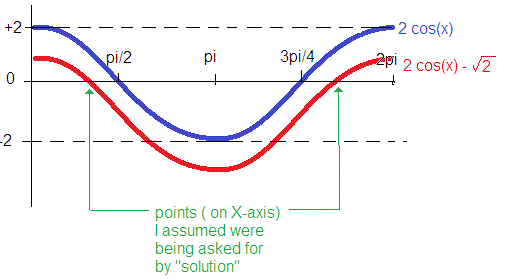
I was not certain what you meant by "solve"; I have assumed you meant:
solve for
(This is a standard #45^o angle)
Within the specified range
when
and
