Question

How do you graph `f(x)=(2x^2+1)/(x^3-x)` using holes, vertical and horizontal asymptotes, x and y intercepts?

Answer 1

We can graph this equation using a sign chart.

Explanation:

First, let's identify the holes, vertical and horizontal asymptotes and x and y intercepts.

Horizontal Asymptotes
Observing the formula, we can see the degree of the denominator is higher than the numerator (The degree is the largest exponent in a polynomial). This means there will be an asymptote at `y=0`.

Vertical Asymptotes
In order to find vertical asymptotes, we muct factor the denominator. Factoring out an `x` from `x^3-x`, we will get `x(x^2-1)`. Equating both answers to 0 will allow us to find our asymptotes.

`x=0`

`x^2-1=0`
`x^2=1`
`sqrt(x^2)=sqrt(1)`
`x=+-1`
`x!=-1,0,1`

`x` can not equal any of these values as they all result in a 0 in the denominator. This will make the function undefined aka asymptotes.

Holes
Holes occur when there is a zero in both the numerator and denominator that will cancel. There are none in this formula.

X-Intercepts
To find x-intercepts, substitute 0 for `f(x)` and solve.

`0=(2x^2+1)/(x^3-x)`

There are no x-intercepts as the equation above would result in imaginary numbers as answers (`(isqrt(2))/sqrt(2),-(isqrt(2))/sqrt(2)`).

Y-Intercepts
To find y-intercepts substitute 0 for `x` and solve.

`y=(2(0)^(2)+1)/((0)^(3)-(0))`

As the denominator equals zero the equation is undefined. Therefore there are no y-intercepts.

Sign Chart
Using the values above, also known as critical values, we will create a sign chart. We do this by sorting the critical values from least to greatest, and surrounding them with `-prop` and `prop`.

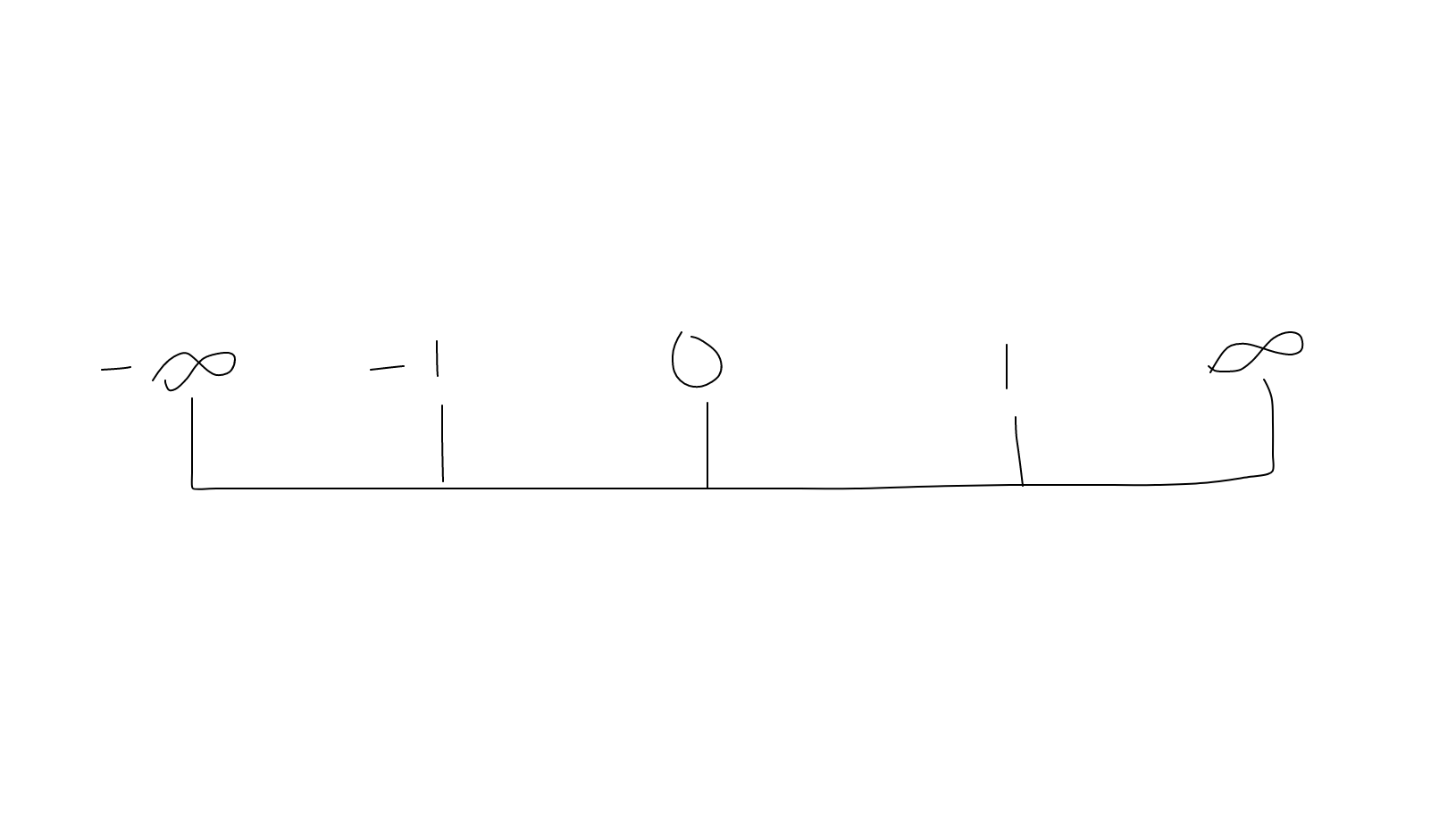
We will then select a value for `x` in between the critical numbers.

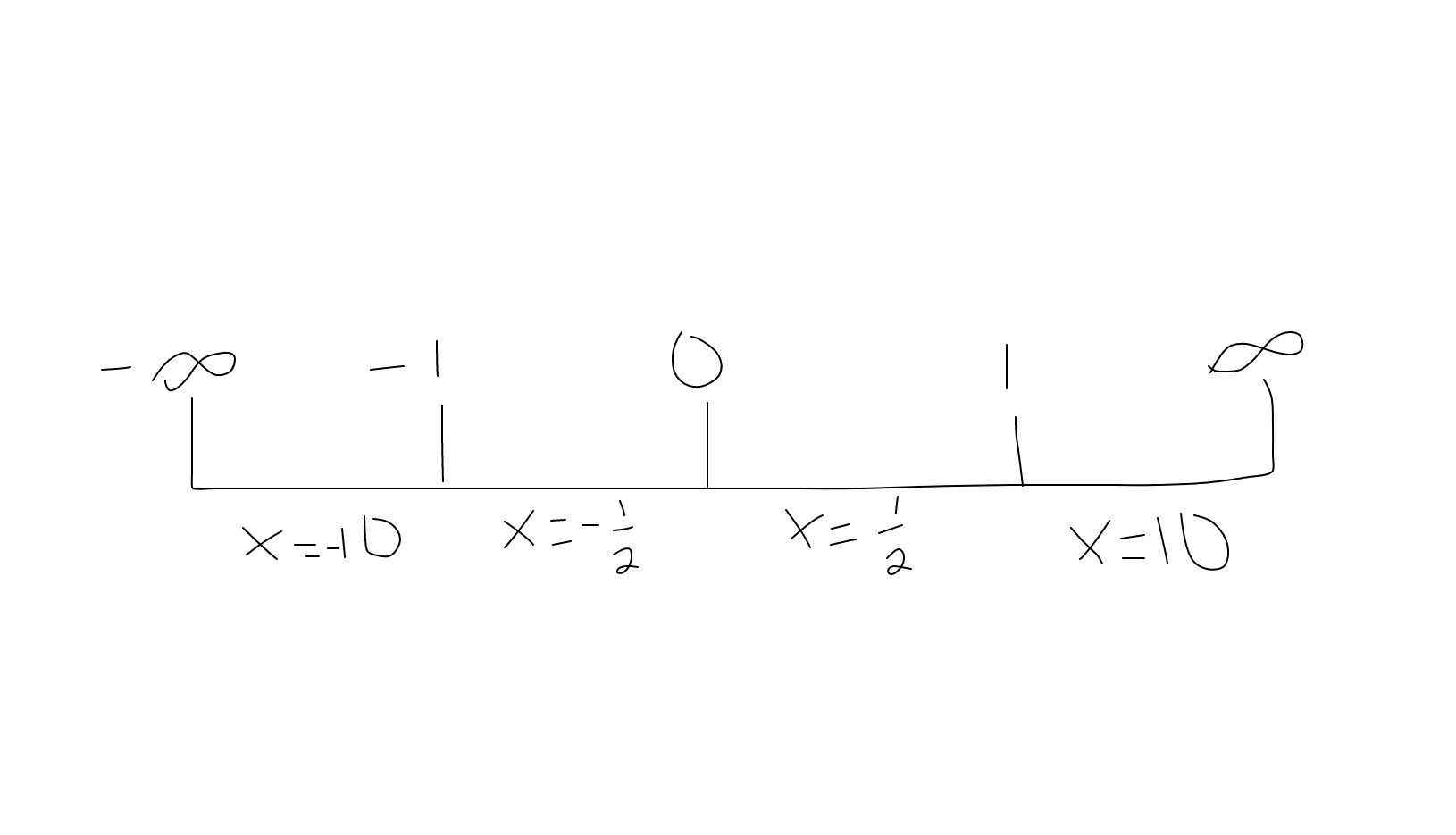
We will test the `x` values for positivity by substituting them for `x` in the formula and write either the positive or negative symbol in the spaces we created. I'll do `x=10` as an example below.
`y=(2(10)^(2)+1)/((10)^(3)-(10))`
`y=67/330`

We don't necessarily care about the value, just whether it is positive or negative. Since it is positive, we will mark a `+` between `1` and `prop`. We will do this for all the values we have chosen.

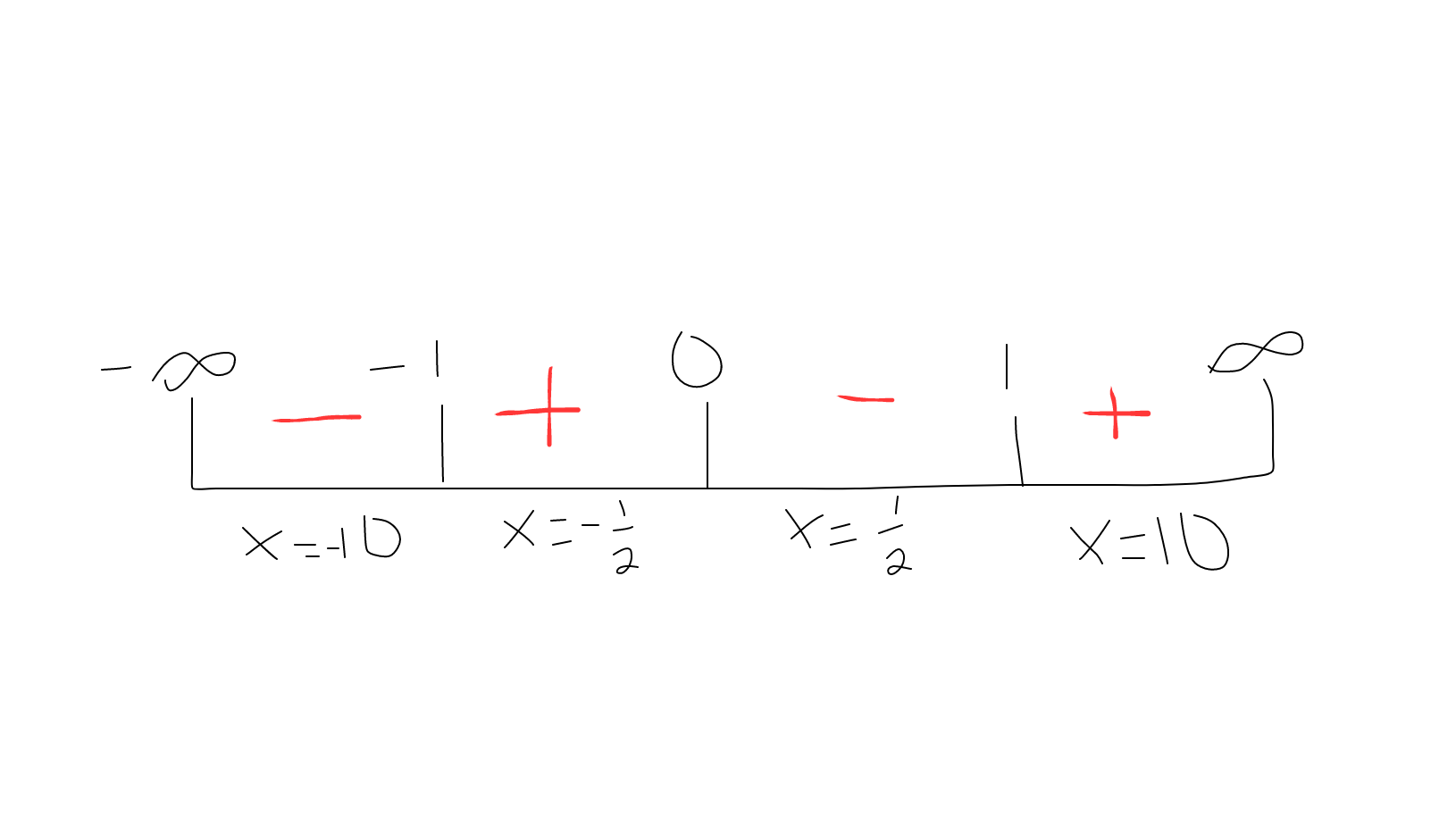
We are now able to graph now that we know where the function is positive and negative and we have the asymptotes.
graph{(2x^2+1)/(x^3-x) [-10, 10, -5, 5]}
Notice how the graph is positive where we noted positive, and negative where we noted negative.