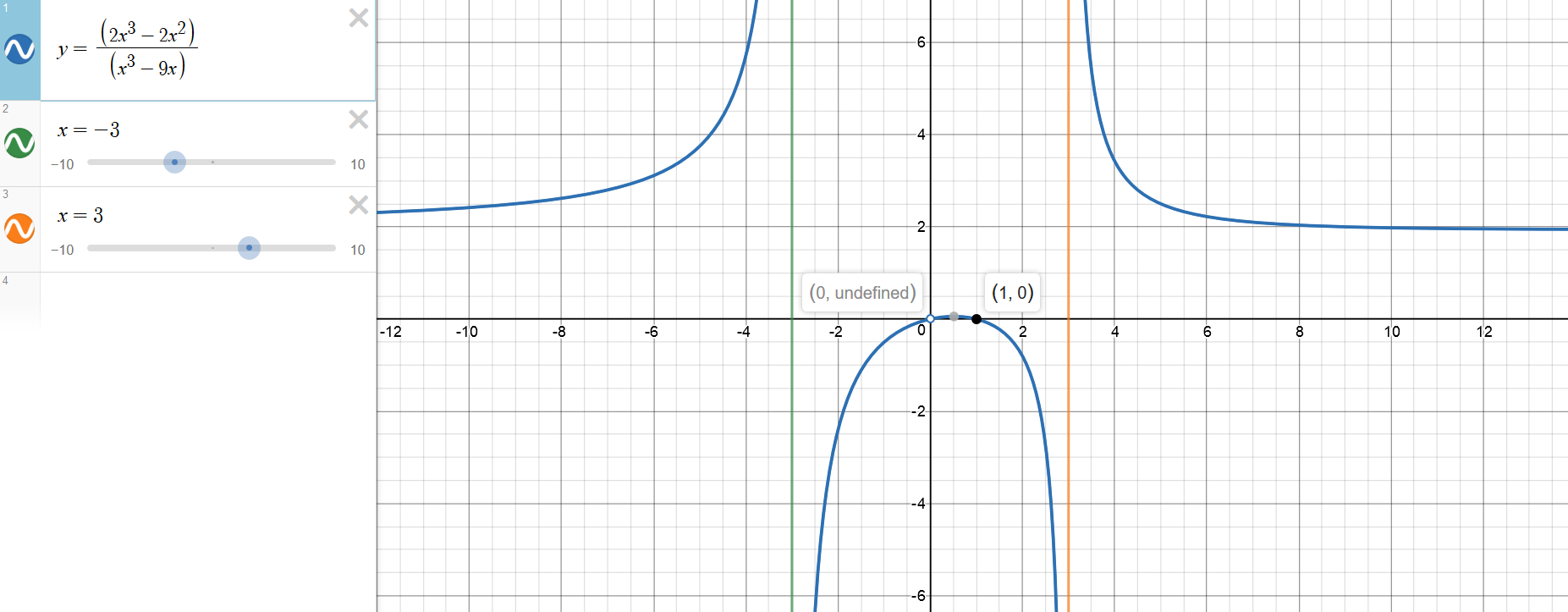
#f(x)=(2x^3−2x^2)/(x^3−9x)=(2x^2(x-1))/(x(x^2-9))=(2x(x-1))/((x-3)(x+3)#
Domain: #RR-{0,+-3}#
Vertical asymptote: #x=3# and #x=-3#
Horizontal asymptote: #y=2#
#y=Lim_(xrarr+-oo)f(x)=Lim_(xrarr+-oo)(2x^3−2x^2)/(x^3−9x)=2/1=2#
Intercepts:
f(x) doesn't intercept y axis because a point #x=0# in not in the domain(We can't divide by 0)
#0=2x(x-1)#
#x=0# makes no sense (it will just seem like it goes through [0,0])
#x=1quadquadquadX_2[1,0]#
I personally wouldn't dare to end it here. Let's find how f(x) behaves in undefined points.
#Lim_(xrarr-3^-)(2x^2-2x)/(x^2-9)=("plus")/("plus")=+oo#
#Lim_(xrarr-3^+)(2x^2-2x)/(x^2-9)=("plus")/("minus")=-oo#
#Lim_(xrarr3^-)(2x^2-2x)/(x^2-9)=("plus")/("minus")=-oo#
#Lim_(xrarr3^+)(2x^2-2x)/(x^2-9)=("plus")/("plus")=+oo#
Notice how function is getting closer in #+oo# to value 2. It is getting closer from below where as in #-oo# is getting closer from above. Therefore it is better to always find that too.
We said that horizontal asymptote is #y=2#. and #Lim_(xrarr3^+)f(x)=+oo# that means: If the fuction approaches y=2 from below it must intercept a line: y=2 in the first place. If we can evaluate a point where function intercepts y=2 that means it is getting closer from below:
#2=f(x)=(2x^2-2x)/(x^2-9)#
#cancel(2x^2)-18=cancel(2x^2)-2x#
#x=9#
Note that #x=9>x=3# (an asymptote) That means we have only one point crossing y=2 which is on right (in #+oo#).
(Note: there are some functions which are getting closer from below in #+oo# and also in #-oo#. If that was the case we would have quadratic funtion)
don't forget undefined point [0,0]