How do you graph #f(x)=-3/(x-1)-1# using holes, vertical and horizontal asymptotes, x and y intercepts?
1 Answer
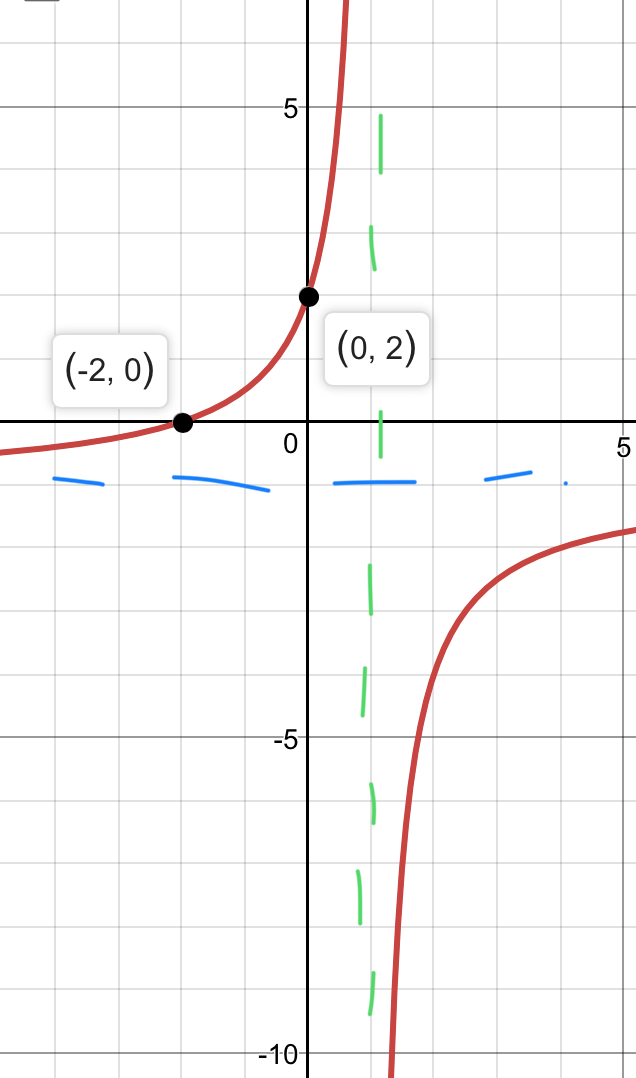
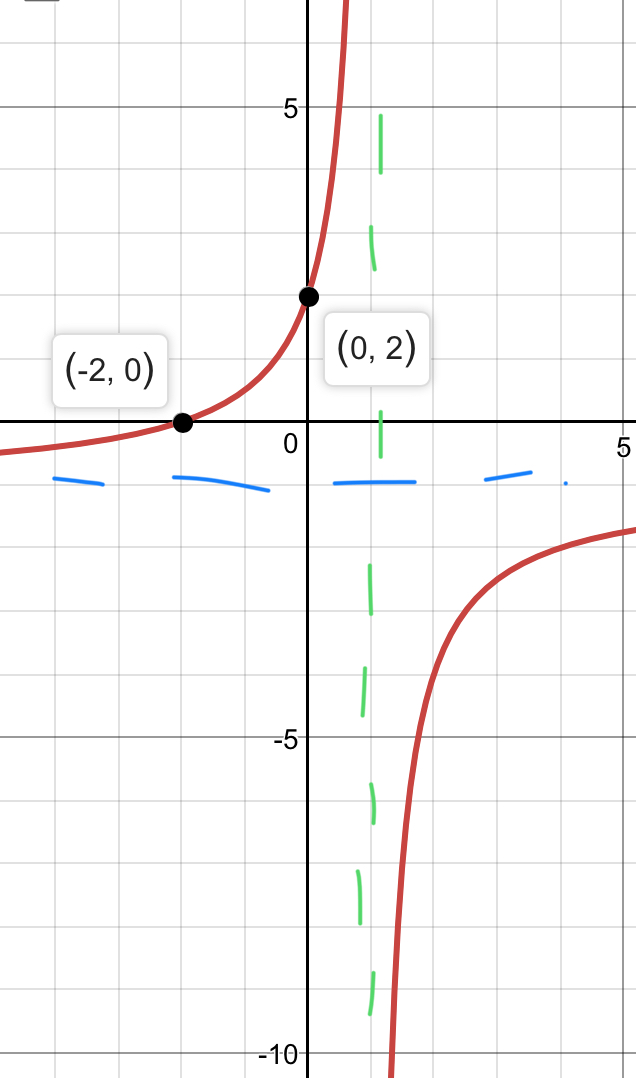
The green line is the vertical asymptote, the blue line is the horizontal asymptote.
Explanation:
Our first step is to make this function completely rational by combining the two fractions:
There are no holes because the factors do not cancel on the top and bottom.
There are vertical asymptotes anywhere the denominator equals zero so:
Since the degree is the same on the top and bottom, the horizontal asymptote is determined by dividing the leading coefficients in the numerator and denominator. So
Find the x-intercept by setting the numerator equal to zero, so
Finally find the y-intercept by setting
After plotting these points and graphing these asymptotes just make sure the curve crosses through these points while also slowly approaching the asymptotes as the graph approaches infinity.