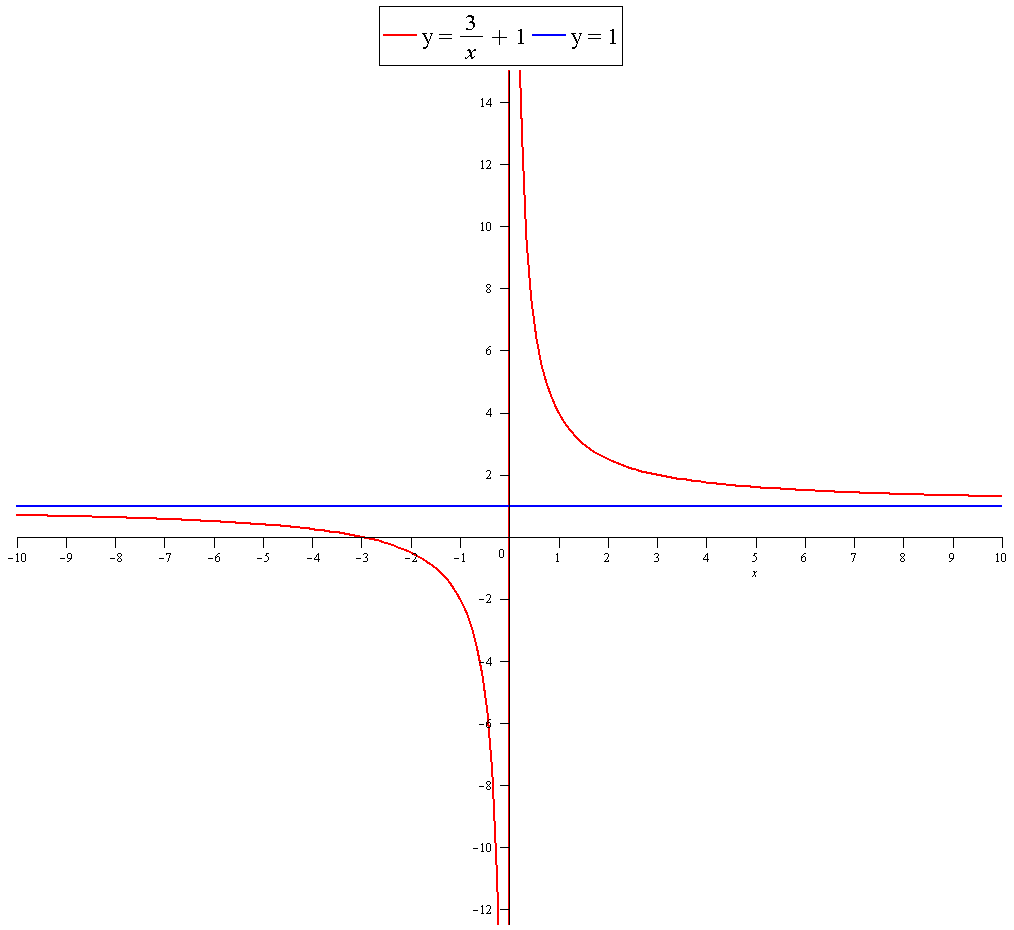
How do you graph #f(x)=3/x+1# using holes, vertical and horizontal asymptotes, x and y intercepts?

Question

1451 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2017-12-05T19:06:31

See below.

y axis intercepts occur when #x=0#. #x=0# is undefined for this function, so no y intercept.

x axis intercepts occur when #y=0#:

#3/x+1=0=>x=-3#

Coordinate: #( -3 , 0 )#

as #x->oo# , #color(white)(888)3/x+1->1#

as #x->-oo# , #color(white)(888)3/x+1->1#

The line #y=1# is a horizontal asymptote.

as #x->0^+# , #color(white)(888)3/x+1->oo#

as #x->0^-# , #color(white)(888)3/x+1->-oo#

The line #x=0# is a vertical asymptote.

Graph:

enter image source here