Question

How do you graph `f(x)=-x^2+3, x>=0` and then use the horizontal test to determine whether the inverse of f is a function?

Answer 1

Graphs of `color(red)(f(x) = -x^2 + 3, " "x>= 0)` and its inverse are available with this solution.

The shaded region clearly indicates `f(x) = -x^2 + 3, " "x>= 0`

Explanation:

Horizontal Line Test will determine whether the Inverse of f(x) is also a function.

When we investigate the graph of `f(x)` we observe that every horizontal line drawn on the graph intersects the function in only ONE location.

Investigate the graph below. I have chosen a few sample values as y = -0.5, y = +0.5, y = +1.5 and x = +2.5 for the horizontal line test. We can see that all these horizontal lines intersect the graph (in the shaded area) in only ONE location.

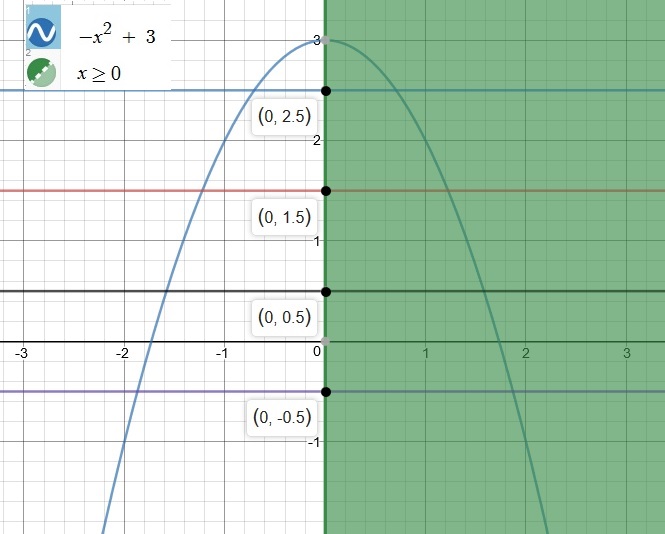
Hence, we can conclude that the inverse of f(x) will also be a function.

we are given `color(red)(f(x) = -x^2 + 3, " "x>= 0)` `color(green)( ..Equation.1)`

To find the Inverse of `f(x)`

Write `color(red)(y = -x^2 + 3`

Switch `x and y` values and make `y` the subject of our equation.

We get

`color(red)(x = -y^2 + 3`

`color(red)(rArr y^2 = - x + 3)`

`color(red)(rArr y = sqrt(- x + 3))` `color(green)( ..Equation.2)`

The inverse of our function `color(red)(f(x) = -x^2 + 3` is given below:

Inverse of `f(x) = sqrt(-x+3) " "`using `color(green)( Equation.2)` above.

To verify our observations, please investigate the graph below:

`color(green)( ..Equation.2)` for inverse is also graphed.

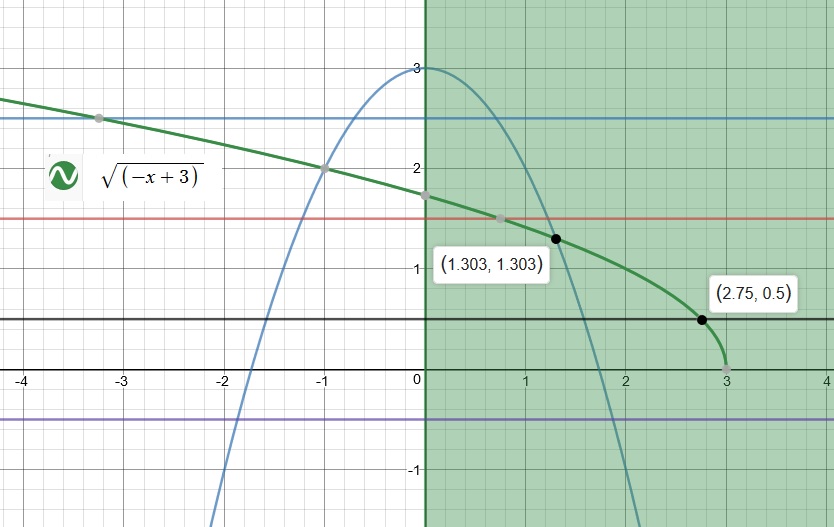
I hope you find the solution useful.