Question

How do you graph `f(x)=(x^2+3x)/(-4x+4)` using holes, vertical and horizontal asymptotes, x and y intercepts?

Answer 1

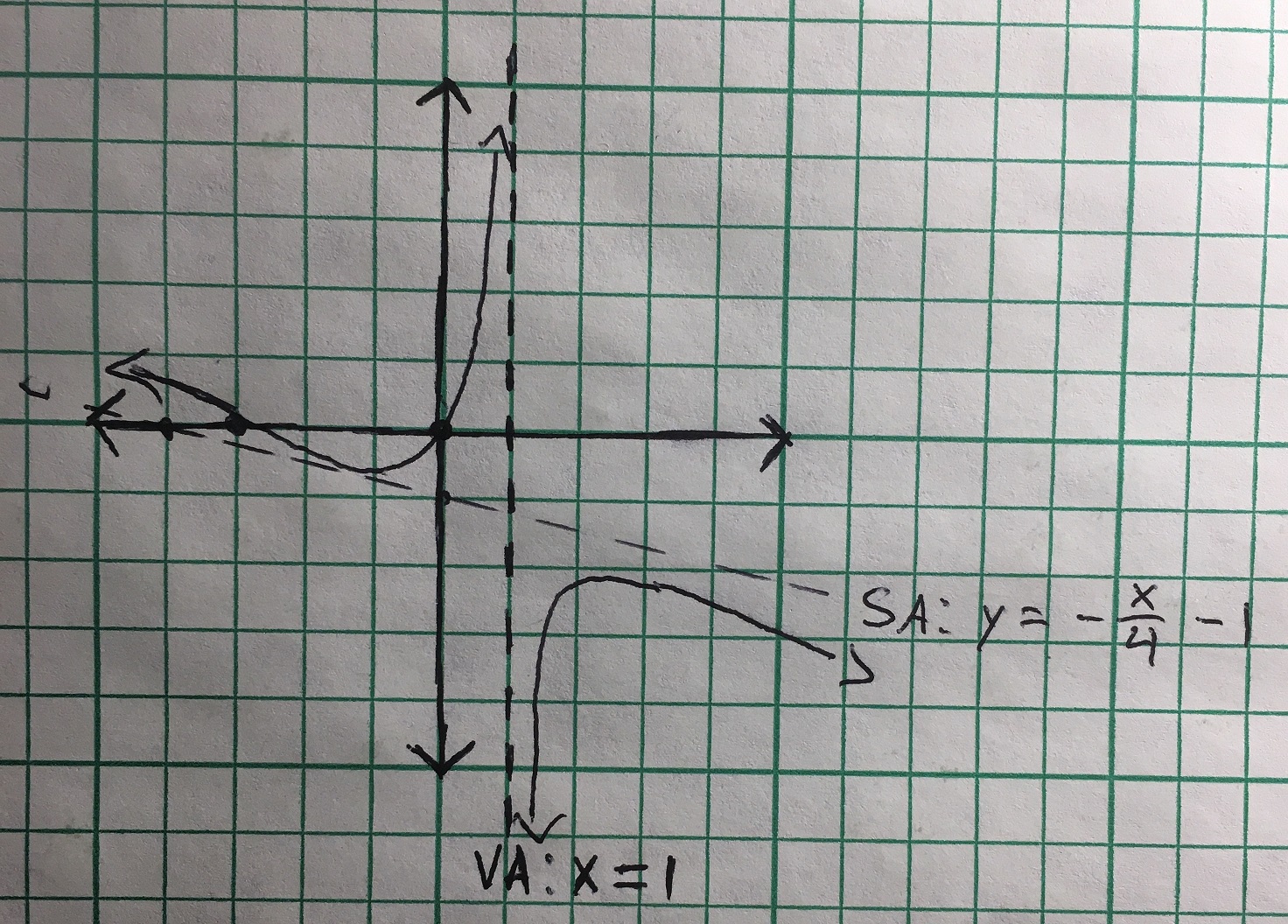
Check below for how to calculate everything necessary to graph the line!

Explanation:

First, I decided to determine the vertical asymptote! You can determine the vertical asymptote by taking the denominator and setting it equal to zero.

`-4x+4=0`

`-4x=-4`

`x=1`

There's a vertical asymptote at `x=1`.

Now for the horizontal asymptote! The horizontal asymptote is determined by looking at the leading coefficients in the numerator and denominator. Here's a helpful visual.

In our case, the leading coefficient in the numerator (`x^2`) is larger than the leading coefficient in the denominator (`-4x`). This means there is no horizontal asymptote!

In some cases, a slant asymptote may be present in a graph. These are sometimes present in graphs that have a stronger leading coefficient in the numerator than the denominator. To determine the slant asymptote, we need to divide the numerator by the denominator.

If you don't know how to do polynomial long division, I'd recommend watching this helpful YouTube video:

Here's how I worked it out:

The slant asymptote is `y=-x/4-1`

Holes are determined by finding numbers that when plugged into x, return undefined. On a graphing calculator these values will give us an error. Luckily for us, there are no holes, so we can move on.

X-intercepts are values that make the numerator equal zero. We can find these by setting the numerator equal to zero and solving.

`x^2+3x=0`

`x(x+3)=0`

`x+3=0`

`x=-3`

Another number that makes the numerator equal zero is, well, zero!

`x^2+3x=0`

`(0)^2+3(0)=0`

`0=0`

So we know our x-intercepts are 0 and -3.

To find the y-intercepts, set x equal to zero and solve the equation!

`y = (x^2+3x)/(-4x+4)`

`y = ((0)^2+3(0))/(-4(0)+4)`

`y = 0/4`

`y=0`

So we have a y-intercept at `y=0`!

Now that we have everything we can graph the equation!

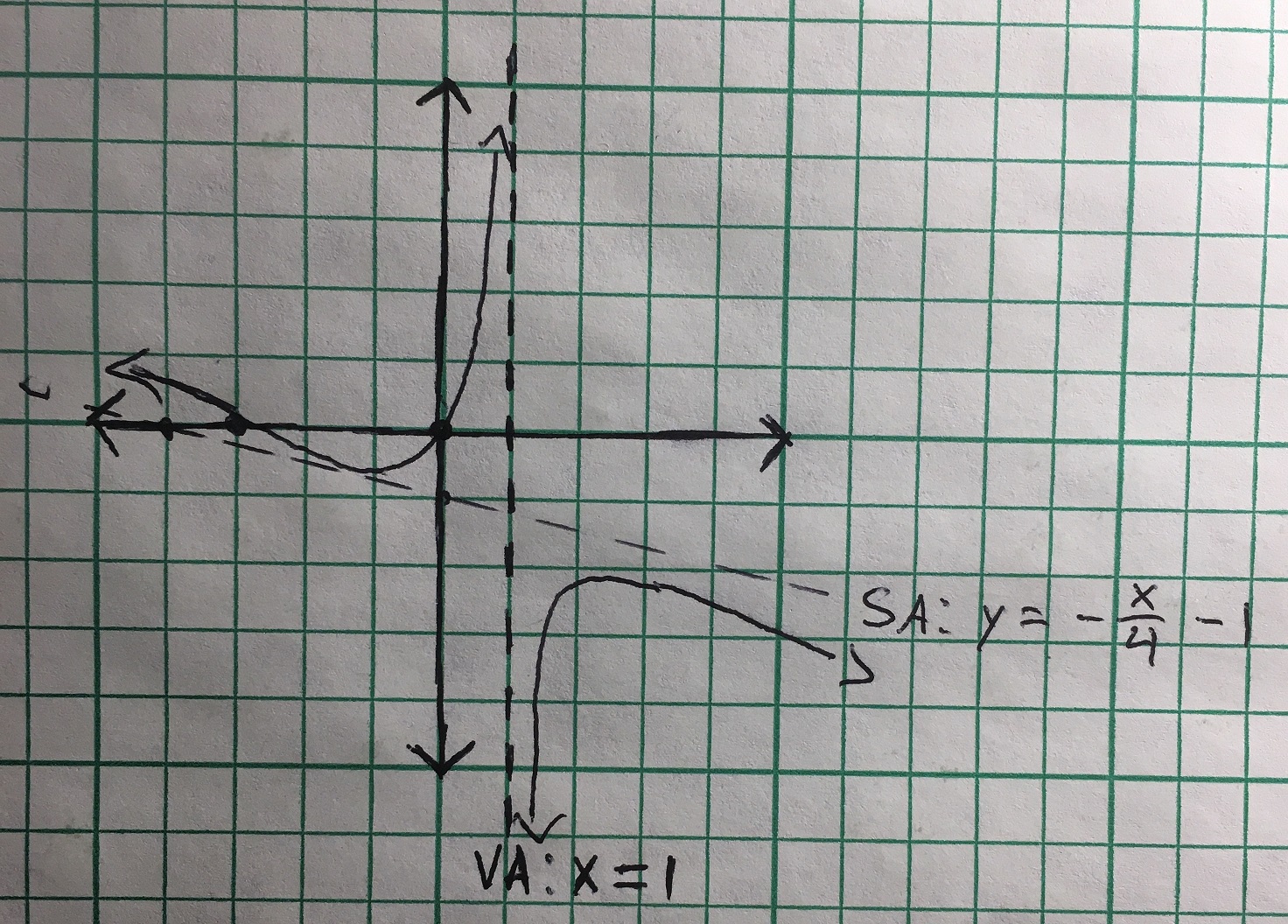
I'm really bad at drawing lines, but you get the idea! Be sure to have your line go through the vertical and horizontal intercepts!