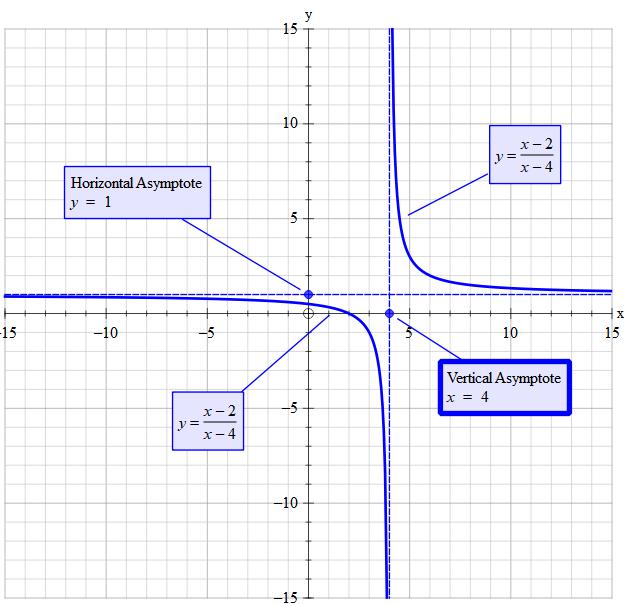
#color(blue)("Hole - undefined")#
Hole is where the denominator becomes 0. The function becomes undefined at that point. So for this condition we have #x=4#
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Lets consider the behaviour close to #x=4#
#color(blue)("Vertical Asymptot "->+oo)#
If #x=4+delta4# where #delta4>0# and very small then we have
#(4+delta4-2)/(cancel(4)+delta4-cancel(4)) ->2/(delta4)+1#
#lim_(delta4->color(white)()^+ 0)2/(delta4)+1 color(white)("dd")->color(white)("dd")kcolor(white)("dd")->color(white)("dd")+oo+1=+oo#
#color(blue)("Vertical Asymptot "->-oo)#
If #x=4-delta4# where #delta4>0# and very small then we have
#(4-delta4-2)/(cancel(4)-delta4-cancel(4)) ->(2-delta4)/(-delta4)=-2/(delta4)+1#
#lim_(delta4->color(white)()^+ 0)-2/(delta4)+1color(white)("dd") ->color(white)("dd")kcolor(white)("dd")->color(white)("dd")-oo+1=-oo#
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
#color(blue)("Horizontal Asymptot "->+oo)#
#(x-2)/(x-4)#
As #x>0# becomes increasing greater and greater the influences of the -2 and -4 become less and less significant. This continues until we have
#lim_(x->+oo) (x-2)/(x-4)color(white)("dd")->color(white)("dd")kcolor(white)("dd") ->color(white)("dd")oo/oo=+1#
As #x<0# becomes increasing less and less the influences of the -2 and -4 become less and less significant. This continues until we have
#lim_(x->-oo) (x-2)/(x-4)color(white)("dd")->color(white)("dd")kcolor(white)("dd") ->color(white)("dd")(-oo)/(-oo)=+1#